Écrivez un programme qui construit le code de Huffman pour l'alphabet exemplaire. Le programme est très court, mais non-trivial, à cause de la récursivité assez avancée.
-
Commencez par la construction de la liste [('a', 2), ('b', 10), ('c', 5), ...] des caractères avec leurs fréquences. On construira l'arbre avec des tuples (sauf si vous préférez construire des classes des arbres, et vous vous sentez prêts à les tester. Vous pouvez toujours jeter un coup d'oeil sur mon cours). La liste ci-dessus est la liste de feuilles.
-
Réduisez la liste en construisant les noeuds intermédiaires. D'abord il faut trier la liste selon le poids de chaque élément : LL=[('a', 2), ('e', 4), ('c', 5), ('j', 6), ('h', 8), ('i', 8), ('b', 10), ('f', 11), ('g', 16), ('d', 21)]. Pour trier une liste il suffit d'évaluer : l1=sorted(l), mais si les éléments sont des tuples, cette commande triera la liste selon le premier élément (indice 0) de chaque tuple, tandis que nous voulons l'indice 1.
On peut essayer l1=sorted(l,
key=lambda x:x[1]). Avec ...,key=fff, la procédure de tri utilise la fonction fff qui doit retourner la valeur selon laquelle les éléments x sont triés. Donc, par ex. le second composant de l'élément. J'ai utilisé une fonction (définie à côté) un peu plus compliquée, si deux éléments ont la même valeur, et un d'eux est une feuille, alors on prend cette feuille. Par exemple, on vérifie le type(x[0]), si c'est str, c'est la fréquence x[1], sinon, c'est x[1]+0.5. Pour l'instant il n'y a que des feuilles, mais cela changera.
On combine les deux premiers items de la liste LL en les combinant dans un tuple, et en calculant le poids correspondant, la somme. Ici on obtient ((('a', 2), ('e', 4)), 6). On répète l'opération, la seconde réduction est ((('c', 5), ('j', 6)), 11). La troisième construit ((((('a', 2), ('e', 4)), 6), ('h', 8)), 14). Après chaque réduction, le nouveau noeud remplace les deux anciens, premiers, et la liste est re-triée. La réduction se termine quand sa longueur devient égale à 1. C'est l'arbre de Huffman.
-
La seconde étape est un parcours récursif de l'arbre, on descend de la racine vers les feuilles : chaque noeud est une paire (D,P), où
P est le poids (pour la racine : 91 dans notre exemple), et D – le tuple des branches descendantes, "gauche" et "droite". Si D n'est pas un tuple, c'est un caractère (la feuille). L'idée est de descendre de la racine vers les feuilles récursivement, et à chaque descente d'un niveau on ajoute '0' à une veriable tampon si c'est la branche gauche, et '1' si c'est la branche droite. Quand on arrive "en bas", le tampon contient le code, et on peut le placer dans un dictionnaire global, par ex. hc['g']='001'.
Le parcours récursif des arbres (et des graphes) est une des techniques fondamentales dans l'algorithmique, vous la verrez encore une dizaine de fois. Quand la procédure récursive se termine, le dictionnaire contient tous les codes.
Exercice 2.
Construisez un document artificiel composé de lettres 'a' – 'j', aléatoires, avec la distribution de fréquences qui suit les chiffres ci-dessus. On a travaillé sur ce problème, vous devez pouvoir le faire vite. La longueur : autour de 1000 caractères (donc, 8000 bits. Ceci n'est pas trop important).
Codez votre document selon la stratégie de Huffman sous forme de chaîne de caractères '0' et '1', et vérifiez sa longueur. Elle ne doit pas dépasser, disons, 3200, sinon quelque chose a mal marché.
Décodez cette chaîne, comparez avec l'original.
Attention, votre dernier exercice obligatoire.
Correction lexicale ; recherche approximative avec BK-trees
Les arbres BK [Burkhard-Keller]
sont des structures arborescentes N-aires (arité quelconque) qui stockent des mots en fonction de leurs distances de Levenshtein, ce qui permet de scanner un dictionnaire et chercher des mots proches de la requête, sans parcourir le dictionnaire entier. Ils ont été inventés en 1973 et continuent d'être utilisés dans les correcteurs, et moteurs de recherche. Voir aussi Wikipédia. Vous trouverez aussi leur implémentation en Python, mais mes avertissements habituels s'appliquent...
Vous devez bien comprendre l'idée de distance de Levenshtein (-Damerau), si ceci vous pose encore des problèmes. Revisez mon cours, copiez éventuellement mon programme leven0.py, lisez le texte de Norvig) mentionné également en cours, ou/et profitez de l'assemblage de plusieurs implémentations de la métrique de Lev-Dam sur le Web.
Supposons que vous cherchez un terme, par ex. "trover". Pardon? "trouer"? "trouver"?... Peut-être trover tout court? On doit trouver une concordance (éventuellement inexacte) avec le dictionnaire (ou vocabulaire) à notre disposition. Dans Textes vous trouverez quelques listes de mots en français, de longueur variée : liste2000.txt, liste_mots.txt, motsfrgut.txt (la seule qui contient "trouer", mais elle est énorme...), et peut-être autre chose, par ex; words2000.txt en anglais. Prenez un vocabulaire plus grand, si votre ordinateur et votre patience résistent, mais pour les tests, choisissez de préférence un petit.
Comme il a été dit in cours, la technique la plus superficielle, serait de comparer tous les mots du vocabulaire avec la requête, et retourner la réussite si le mot est proche, éventuellement arrêter la comparaison, si la distance L-D dépasse un seuil, disons 2 ou 3. Mais ceci serait aussi inefficace, surtout si les requêtes se succèdent. J'ai dit en cours qu'une méthode d'optimisation serait de "gonfler" (en pré-traitement) le vocabulaire avec des mots distordus, mais ceci est explosif, demande une très grande mémoire même pour les mots très proches. On procédéra autrement.
Vocabulaire arborescent conceptuel
Dans le domaine de recherche informatisée (en général) les arbres sont des structures fondamentales, à cause de la "logarithmisation" du temps de parcours. Au lieu de parcourir séquentiellement une structure linéaire, si un mécanisme décisionnel approprié est implémentable, alors on construit un arbre avec les données, et on suit (dans le cas optimal) une seule branche, ce qui logarithmise la complexité du procédé. Un exemple banal, connu de tous, est la structuration d'un dictionnaire classique (ou d'une encyclopédie). Le dictionnaire est trié, et notre "algorithme humain" nous permet d'"aller à gauche" ou "à droite", et trouver le mot assez rapidement (c'est mieux que \(\log_2\) de la longueur, car nous savons qu'un mot en "d" se trouve pas loin du début, etc. ; on n'a pas besoin d'ouvrir le dictionnaire au milieu). Ce sujet a été discuté en cours de Python maintes fois, déjà en L1.
On n'a pas besoin toujours de la construction physique d'un arbre, pour appliquer un algorithme arborescent, parfois c'est la dynamique récursive qui fait l'affaire. Cependant ici, c'est l'approche la plus naturelle.
L'ordre alphabétique peut être très utile, mais il n'est pas pertinent pour la recherche approximative, car même la première lettre peut être erronée. On utilisera la distance L-D pour l'algorithme de construction et de recherche. La distance de Levenshtein servira pour étiqueter les branches dans l'arbre.
Construction de l'arbre BK
Les noeuds de notre vocabulaire arborescent sont des mots, et les branches étiquetées par \(N\) mènent vers les noeuds "distants" de \(N\) du noeud en question. La structure globale de l'arbre dépend de l'ordre de l'insertion des nouveaux noeuds. L'arbre sera \(N\)-aire, chaque noeud sera associé à une liste de \(N\) descendants.
Si vous voulez utiliser une classe d'arbres Python, faitez-le, mais une solution plus simple est possible.
-
L'arbre est un dictionnaire, les clés sont des mots.
-
La valeur correspondante est une liste. Chaque élément de cette liste est une paire (N,Md), où N est la distance, et Md est le mot descendant, le premier mot de cette distance, inseré depuis la racine. Les autres seront attachés "plus loin".
-
Le mot Md sera placé dans le même dictionnaire, pas besoin d'une hiérarchie imbriquée.
-
Un mot-feuille de l'arbre est associé à la liste vide.
-
La construction de l'arbre commence par
bkdict={Rac : []}, où Rac est la racine, le premier mot inséré dans le dictionnaire.
-
L'insertion d'un nouveau mot Md procède depuis la racine. On vérifie la distance N entre Md et la Rac, et on vérifie si la liste associée à Rac possède l'étiquette égale à N. Si non, alors on insère dans cette liste la paire (N,Md).
-
Si cette branche existe déjà, si on trouve la paire (N,Xx), alors on lance la procédure d'insertion récursivement, on insère Md en prenant Xx comme racine.
Exemple.
 Prenons la liste
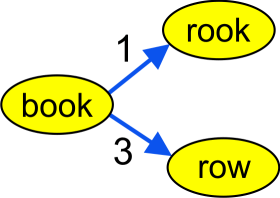
Prenons la liste ['book','rook', 'row', 'boom', 'how']. La racine de l'arbre est 'book'. L'insertion de 'rook' et ensuite 'row', donne le résultat à gauche.
Dans notre représentation, le dictionnaire contient {'row': [], 'rook': [], 'book': [(1, 'rook'), (3, 'row')]}.
Si on insère 'boom', on constate que la branche 1 est déjà occupée par 'rook', et donc il faudra insérer le nouveau mot ici. On calcule la distance entre 'rook' et 'boom', qui est 2. Le mot 'how' est associé à 'row' avec distance 1.
Le dictionnaire devient {'boom': [], 'row': [(1, 'how')], 'how': [], 'rook': [(2, 'boom')], 'book': [(1, 'rook'), (3, 'row')]}.
Voici sa forme graphique :
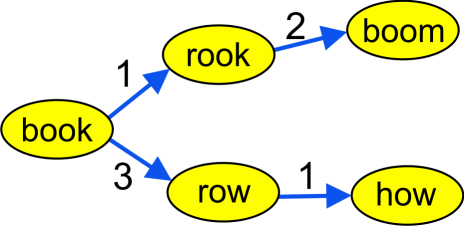
L'arbre final est assez irrégulier, mais normalement devra économiser beaucoup de temps de recherche. Par contre, la construction est assez onéreuse, la complexité est proportionnelle à \(m^2\), où \(m\) est la taille du vocabulaire. Dans mes tests, un vocabulaire de 22600 mots demande quelques dizaines de secondes pour la conversion en arbre [on peut faire mieux !], mais pas plus. Donc, ne commencez pas par une liste longue de plusieurs centaines de milliers de mots !
La recherche
La procédure devra trouver tous les mots dans le vocabulaire, dont la distance de la requête ne dépasse pas un certain seuil \(d\), par ex. 2 ou 3. On commence par la racine. Chaque mot trouvé est accumulé dans la liste - résultat. Cette liste est retournée comme le résultat de recherche.
La procédure de recherche est récursive. On vérifie si la distance \(n\) entre le mot cherché et la racine de l'arbre est inférieure ou égale à \(d\). Si oui, comme il a été dit, on accumule le mot - racine et on continue, sinon on continue sans ajouter quoi que ce soit.
La continuation est le parcours par toutes les branches de la racine, et la recherche parmi les descendants. Mais on ne vérifie pas la liste complète ! Si la distance entre la racine et le mot cherché est \(n\), alors les candidats éligibles ont la distance entre \(n-d\) et \(n+d\). Seulement les branches étiquetées avec ces nombres seront pris en considération, les autres sont ignorées. Pour chaque mot descendant, on relance la procédure récursive. (La liste - résultat est globale, et accumule tout, mais on peut aussi concaténer les listes locales). L'efficacité de la procédure est raisonnable même en Python.
Par ex., si on cherche dans la liste de 23000 mots mentionnée ci-dessus le mot "schtroumpf" avec la tolérance 4, on ne trouve rien, et la recherche dure approx. 6 secondes. (Avec la tolérance 1, la réponse est immédiate).
Plusieurs optimisations sont possibles, on peut trier la liste - branche, utiliser les tableaux avec l'accès plus rapide, et autres dispositifs, mais l'essentiel est que ça marche.
Exercice 3.
Récapitulatifs, Tests
-
Prendre une liste de mots, une de listes sauvegardées par moi, ou sur l'Internet, par ex. ici, ou ailleurs. Lire la liste dans la mémoire, elle doit être correctement codée, sans parasites (par ex. fins de ligne), etc.
-
Coder la procédure qui construit l'arbre BK depuis une liste de mots. Faire l'arbre, d'abord d'une courte liste - test, vérifier soigneusement si la procédure est correcte, et construire l'arbre final.
-
Opération auxiliaire. Sauvegarder le dictionnaire obtenu sur le disque, en utilisant les dispositifs Python de sauvegarde des objets : pickle (binaire) ou json (textuel). Ainsi pour la recherche, le débogage évitera la construction à nouveau...
Vous devez sauvegarder le dictionnaire ET son mot - racine, par ex. dans un tuple. Le dictionnaire ne sait pas quel mot est la racine... [On peut lui ajouter cette information, par ex. ajouter un élément artificiel, bk[0]='book', mais il faut s'assurer qu'un parcours du dictionnaire ignore cet item].
Ceci n'est pas indispensable, mais c'est facile, et permettra de séparer la construction de l'arbre, et le codage de la recherche, sans gaspiller le temps pour le reconstruction de la structure BK. Je vous rappelle...
Si vous avez un objet X Python, le programme suivant :
import pickle as pk # Le module de sérialisation/récupération
fp=open('data.dp',"wb") # Extension arbitraire ; évitez la confusion avec d'autres formats
pk.dump(X,fp) # Lisez la doc du module pickle.
sauvegarde une structure complexe Python sous une forme récupérable. Dans un autre programme, vous exécutez :
import pickle as pk
fp=open('data.dp',"rb")
X=pk.load(fp) # Dans le même endroit que "dump"
-
Écrivez une procedure bkrecherche(Mot,maxd) qui trouve dans l'arbre - vocabulaire tous les mots dont la distance du Mot ne dépasse pas maxd. Les programmes doivent être dûment commentés.
-
Testez pour au moins une vingtaine d'exemples donnant les résultats très différents, avec
maxd variant de 1 jusqu'à 4 ou 5.
Vous avez le temps jusqu'à la fin du semestre (date à préciser, provisoirement : fin des cours, début des vacances de Noël)
Solutions (à venir)
Semaine suivante
Retour à l'index
 Prenons la liste
Prenons la liste 