Le point de départ de la construction d'une regexp "pair a pair b" correspondant à l'automate à droite, [lisez les exercices de la semaine dernière] est l'ensemble d'équations :
Les grammaires non-contextuelles (vous aurez la signification de ce mot un peu plus tard) ont été (/ auraient dû être) mentionnées en cours, aujourd'hui quelques simples exercices, mais on reviendra plus tard aux grammaires plus compliquées, traitées par NLTK.
Ici nous allons jouer avec les DCG (Direct Clause Grammars) implémentées en Prolog, concrètement en SWI-Prolog, un langage de programmation logique, utile pour les non-"numériciens" de toute spécialité, y compris les sciences humaines. Je ne sais pas encore si dans s.122 l'installation du SWI a été actualisée, mais les concepteurs ont prévu un serveur Web Prolog [restreint], permettant de faire des simples exercices directement en ligne. (Bien sûr, si vous installez SWI chez vous [5 minutes], tant mieux. Vous avez au moins 5 autres implémentations gratuites de Prolog sur le Web, celle-là est une de plus populaires et vivaces).
Prolog est un langage pour la manipulation des données symboliques, il a été conçu dans le cadre de la recherche linguistique, et si vous n'aviez pas été "conditionnés" par Python, cela aurait été notre langage de travail. Voici un peu de doc.
Rappelons l'idée de base. Une grammaire est un ensemble de règles contenant des motifs, ou "patterns" qui sont compatibles avec le texte reconnu ; conceptuellement ceci ressemble aux regexps, même si la formulation est différente, et les grammaires sont considérablement plus universelles.
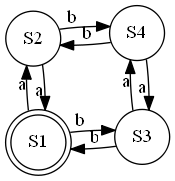
Le point de départ de la construction d'une regexp "pair a pair b" correspondant à l'automate à droite, [lisez les exercices de la semaine dernière] est l'ensemble d'équations :
S1 = ε S1 = S2 a | S3 b S2 = S1 a | S4 b S3 = S1 b | S4 a S4 = S2 b | S3 aet ceci est une grammaire dans un format un peu bâtard... les états S sont des "variables syntaxiques" appelées souvent "non-terminaux", et les symboles a, b - des constantes, ou terminaux. Un non-terminal spécifié, l'état de départ de la reconnaissance, est distingué. (Ici c'est S1 ; accessoirement il est également l'état final).
Rappelons une grammaire "(a|b)*" en DCG Prolog montrée en cours :
aoub --> [a] | [b]. etoile --> [] | aoub,etoile.Les symboles entre crochets, et en minuscules (ou entre apostrophes) sont des "atomes", des terminaux, et correpondent aux transitions. Les mots dehors sont des variables syntaxiques. La virgule symbolise la concaténation. Le programme (plus simple qu'en cours) :
phrase(etoile,[a,a,a,b,b]).répond : true. L'échec sera false. Les complications arrivent quand nous voulons récupérer le fragment qui a été reconnu, ou/et le reste de la chaîne, si on veut procéder en plusieurs étapes (reconnaitre les mots dans une phrase, des phrases dans un texte, etc.), et en général, si on veut faire plus de travail avec les textes que de répondre "oui" ou "non". Mais les grammaires peuvent être construites, comme ici, par combinaisons d'éléments plus simples, utiliser la récursivité, etc. Pour effectuel un calcul quelconque parune grammaire DCG, il faut y insérer une construction { ...}, où entre les accolades on place un morceau de programme Prolog général. Ceci demande une certaine, superficielle connaissance du Prolog.
aoubp(X) --> [X],{X=a;X=b}.
etoilp(Tx) --> [],{Tx=[]}| aoubp(D), etoilp(Frag),{Tx=[D|Frag]}.
et sa trace :
phrase(etoilp(Res),[a,b,a,b,b,a]). Res = [a,b,a,b,b,a]La syntaxe de Prolog est simple, mais à cause de son évolution historique, on y trouve des incongruités. Dans Prolog pur ";" est "OU", et "|" construit des listes, la forme [T|Q] symbolise une liste dont la tête (premier élément) est T, et tout le reste, la queue : Q. Mais dans DCG "|" signifie également "OU" (sauf dans les listes)... Ci-dessus, aoubp "attrape" le caractère trouvé, et etoilp – la liste entière. Une autre manière d'écrire la même définition, est
aoubp(a) --> [a]. aoubp(b) --> [b]. etoilp([]) --> []. etoilp([D|Q]) --> aoubp(D),etoilp(Q).Il vous faudra s'habituer à ces variantes de syntaxe. Ceci vous sera utile en toute indépendance de cette option. Ne confondez pas une liste-singleton avec son seul élément.
La phrase(gram,txt) cherche à reconnaître le texte complet comme conforme à la grammaire. Cependant le processus d'analyse peut être, et d'habitude est incrémental, on trouve par ex. un seul mot dans le texte, on le retourne, et dans une boucle on cherche d'autres mots, ou autre choses. Pour cela nous avons la possibilité d'ajouter le troisième argument, une variable Prolog, par ex. phrase(gram,txt,Reste), et cette variable Reste attrape le reste du texte, après la reconnaissance de la clause grammaticale, comme le prefixe.
Après la réponse de la part de Prolog, si l'utilisateur tape ";" sur le clavier, ceci est la demande "cherche d'autres choses", et Prolog essaie de trouver les solutions alternatives. Ainsi (avec les points-virgules faites par l'utilisateur)
phrase(etoilp(Res),[a,b,a,b,b,a],Reste).
Res = [],
Reste = [a,b,a,b,b,a] ;
Res = [a],
Reste = [b,a,b,b,a] ;
Res = [a,b],
Reste = [a,b,b,a] ;
Res = [a,b,a],
Reste = [b,b,a] ;
Res = [a,b,a,b],
Reste = [b,a] ;
Res = [a,b,a,b,b],
Reste = [a] ;
Res = [a,b,a,b,b,a],
Reste = [] ;
false.
et
phrase(etoilp(Sol),[a,x,b,c,b,d,a],Reste).
Sol = [],
Reste = [a,x,b,c,b,d,a] ;
Sol = [a],
Reste = [x,b,c,b,d,a] ;
false.
L'ordre des solutions dépend de l'ordre des clauses et des éléments dans la grammaire. Parfois ceci est arbitraire, parfois figé par des contraintes d'associativité.
L'automate "pair a pair b" se représente comme la grammaire ci-dessous. Nous avons modifié des règles avec un non-terminal à gauche, qui risquent le plantage récursif, en faveur des règles qui forcent d'abord la reconnaissance d'un terminal. Ceci parfois est conventionnel, l'essentiel est de comprendre comment cela marche : [a],S doit reconnaître a d'abord, ensuite appliquer S.
start --> s1. s1 --> [] | [a],s2 | [b],s3. s2 --> [a],s1 | [b],s4. s3 --> [b],s1 | [a],s4. s4 --> [a],s3 | [b],s2.
Exercice 1.
K = 3*M est légal aussi, mais affecte à K la forme 3*M, sans effectuer l'opération arithmétique.)
Exercice 2.
nom --> [chien] | ['Jean'] | [président] | [acarien]. verbe --> [agresse] | [aime] | [mange]. artdef --> [le]. artind --> [un]. adject --> [intelligent] | [enragé] | ['très sympa']. optadj --> adject | []. sent --> artind,nom,optadj,verbe,artdef,nom.reconnaît des phrases comme : [un, acarien, 'très sympa', agresse, le, président].
phrase(sent,Quelconque). ?
Exercice 3.
an bn", c'est à dire : ε ab, aabb, aaabbb, aaaabbbb, ... etc. Pensez-vous que ceci pourrait être résolu avec les expressions régulières?