LTAL, TP 19.10

Grammaires attribuées

(Ceci complète un peu le cours...)
Comme il a été dit et souligné en cours, une grammaire qui accepte ou non une phrase, est peu utile pratiquement, normalement le processus de parsing doit reconnaître la phrase de manière constructive : assembler l'arbre syntaxique, calculer la valeur d'un nombre, compiler une expression algébrique en code, afficher une carte géographique selon sa description textuelle, etc. Aussi, si le parsing échoue, normalement on doit savoir pourquoi, et où, dans quel contexte.

Les non-terminaux définis par

syntvar(XXX) --> ...

possèdent des paramètres, qui peuvent être transmis d'un appel à l'autre. La variante vue, et très simple (régulière), qui assemble une séquence depuis ses éléments, peut être

sequ([X|Q]) --> elem(X),sequ(Q).
sequ([]) --> [].

où, par exemple :

digit(X) --> [X],{member(X,[0,1,2,3,4,5,6,7,8,9])}.
elem(X) --> digit(X).

(Observez que si les clauses du prédicat sequ sont dans cet ordre-là, on cherche d'abord la phrase la plus longue. Aussi, ne vous trompez pas : dans cet exemple les chiffres sont des nombres, et non pas des caractères). Dans le cours nous montrons comment assembler les chiffres de manière numérique, et donner la réponse numérique, et aussi comment travailler avec les arbres syntaxiques d'une grammaire "linguistique". On parlait de la synthèse des attributs, ou d'attributs synthétisés l'analyseur se lance, son "corps" à droite analyse les fragments, construit des attributs partiels (valeur du chiffre, valeur de la sous-séquence), et ensuite transmet ces informations à la réponse, le paramètre à gauche.

L'assemblage des nombres entiers montre les dangers de la récursivité à gauche. Ce programme déclenche une exception (Out of local stack) :

seqn(R) --> seqn(Q),elem(X),{R is 10*Q+X}.
seqn(0) --> [].

mais on peut éviter cela, si on applique un autre algorithme, exemplifié par le calcul de la valeur de "2031". On sépare le premier chiffre, "2", on calcule la valeur du reste ("031" doit retourner 31), et on assemble le résultat par 2*10³ + 31. L'exposant 3 est calculé comme la position de droite de ce chiffre, ce qui est longueur de la chaîne restante "031" !
Donc, on applique la récursivité à droite (en séparant le premier chiffre, et en récurrant la queue), mais on ne connaît pas la position du chiffre ! Il faut consommer le reste, trouver la longueur (et pas seulement la valeur) de ce reste, et faire récupérer cette longueur par le voisin, le chiffre à gauche du reste. Le calcul des puissances de 10 est peu efficace dans la pratique, mais conceptuellement, le problème est intéressant.

La solution n'est pas trop élégante, mais comme tous nos algorithmes, très courte. elem(X) c'est le chiffre, comme auparavant.

seqr(V,Lng) --> elem(X),seqr(V1,Ln1),{Lng is Ln1+1,V is X*10^Ln1 + V1}.
seqr(0,0) --> [].

L'exécution :

 ?- phrase(seqr(A,N),[2,0,4,8,7,3,m],R).
A = 204873,
N = 6,
R = [m]

(et si on demande encore, on obtient 20487, puis 2048, etc.) On dira ici que l'attribut X reconnu par elem, a été hérité par seqr On peut le mettre dans les paramètres.
Dans le programme présenté en cours :

nmbr(Val) --> nmbr(Val,0).
nmbr(Val,Tmp) --> elem(M),{Tmp1 is 10*Tmp+M},nmbr(Val,Tmp1).
nmbr(Val,Val) --> [].

l'attribut Tmp est aussi hérité, du "parent" à gauche, vers la droite.

Exercice 1.

Écrire une grammaire qui accepte des nombres de zéro jusqu'à 200 : "vingt trois", "sept", "quatre-vingt seize", "trente", "soixante douze", ... et qui en reconstruit les valeurs : 23, 7, 96, 30, 72, ... Simplifiez un peu, ne faites pas la distinction entre "cent" et "cents", "quatre-vingts" et "quatre-vingt". Bien sûr, utilisez les mots comme terminaux, non pas les caractères : ... [vingt, trois], pas de tiret entre les deux mots, mais "dix-huit" est un mot. (Ceci dit, attention, le tiret est un opérateur en Prolog, et le terme : soixante-douze n'est pas un atome, mais un terme fonctionnel, qui s'affiche soixante-douze, pas d'arithmétique.)

Le programme ne doit pas accepter des illégalités comme "trente dix-sept". Ne pas oublier que la phrase "trente un" est mauvaise, on doit dire "trente et un". Cependant : "quatre-vingt un", sans "et". Comme d'habitude, les exceptions qui cassent la régularité, demandent beaucoup de travail... Commencez de manière "tolérante", sans forcément respecter toutes les règles de manière rigide ; l'essentiel est que le résultat soit lisible.

Continuation...
Est-ce que votre programme de reconnaissance est capable également de synthétiser les nombres "textuels"? Si non, identifiez les raisons.

Exercice 2.

Encore une fois un exercice très simple, sur la structure lexicale des phrases... Vous savez comment faire un simple 'tokenizer' en Python : si la phrase (chaîne) est composée de mots - séquences de lettres, séparées par des espaces, par ex. "Belle marquise vos beaux yeux me font mourir d'amour" (gérez l'apostrophe comme vous voulez...), il suffit un seul split pour la séparer (et split existe aussi en Prolog...). On peut utiliser le module re, et chercher les mots via search ou findall. Mais comment le faire de manière "syntaxique" avec les DCG?

Vous avez deux prédicats auxiliaires :

atom_string(Chaîne,Atome), capable de convertir en deux sens.
atom_chars(Atome,Liste_deChars), un autre convertisseur.

Ceci vous éliminera la galère d'écrire ['B',e,l,l,e,' ',m ...]. Si vous sentez besoin d'utiliser d'autres utilités prédéfinis, comme la concaténation des chaînes, etc. lisez la documentation, ou posez des questions.

Écrire une grammaire DCG qui sépare les mots, et qui retourne une liste de ces mots, assemblés en atomes depuis des listes de caractères. Attention, une expression qui définit mot comme une séquence quelconque de lettres, peut – si on n'ajoute aucune autre contrainte – s'arrêter au milieu d'un mot. Ceci est considéré erroné. L'analyse d'un mot doit itérer jusqu'à la fin de ce mot, on n'a pas le droit de s'arrêter avant. Ceci n'est pas entièrement trivial.

Enfin, NLTK...

Ce paquetage, mentionné plusieurs fois, mais jamais utilisé en TP, est devenu une sorte d'Arlésienne de nos travaux. (Si vous ne connaissez pas le terme "Arlésienne" jadis présent dans la culture populaire française [Daudet, 1866], éduquez-vous...) On revient à Python.

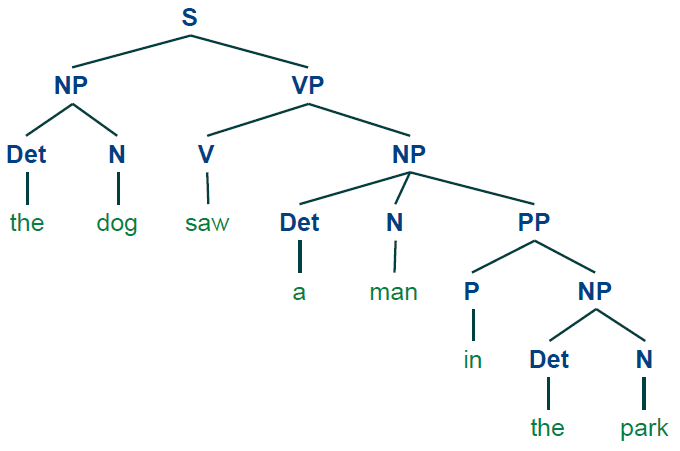
En cours nous avons montré le programme ci-dessous. Vérifiez s'il marche !

import nltk

grammar1 = nltk.CFG.fromstring("""
  S -> NP VP
  VP -> V NP | V NP PP
  PP -> P NP
  V -> "saw" | "ate" | "walked"
  NP -> "John" | "Mary" | "Bob" | Det N | Det N PP
  Det -> "a" | "an" | "the" | "my"
  N -> "man" | "dog" | "cat" | "telescope" | "park"
  P -> "in" | "on" | "by" | "with"
  """)

sent = "the dog saw a man in the park".split()

rd_parser = nltk.RecursiveDescentParser(grammar1)

for tree in rd_parser.parse(sent): 
    print(tree)

Ceci affiche

(S
  (NP (Det the) (N dog))
  (VP
    (V saw)
    (NP (Det a) (N man) (PP (P in) (NP (Det the) (N park))))))

et la méthode tree.draw() affiche le dessin dans une fenêtre tkinter.

Exercice 3.

Cet exercice est aussi consacré à la reconnaissance d'un langage formel plutôt que naturel, pour la simplicité. Il faut d'abord savoir traiter des cas simples, avant de se lancer dans le domaine, où rien n'est vraiment sûr.

Écrire une grammaire NLTK permettant d'analyser les listes Python, restreintes. Tester la grammaire sur des cas légaux et illégaux. Voici la définition d'une liste légale

Une liste peut être vide : [].
Elle peut contenir UN élément : [Elem],
ou, une séquence d'éléments séparés par des virgules : [El1,El2, ... , El_n] ; on ne peut ni commencer ni terminer la séquence par la virgule.
Un Élément peut être un nombre entier - séquence de chiffres.
Un Élément peut être une chaîne - séquence de caractères délimitée par des guillemets : ("). Pas de cas spéciaux (guillemet interne), les apostrophes sont considérés comme des caractères ordinaires.
Ou, un tuple de deux, ou trois éléments (rien d'autre, sauf si vous insistez) : (X,Y) ou (X,Y,Z), ou X,Y,Z sont des Éléments immuables (nombres ou tuples, mais pas de listes !).
Ou, (vous avez deviné...) un dictionnaire Python : {clé : valeur, ... }. Les clés doivent être obligatoirement des chaînes, sinon la structure n'est pas acceptée. Les valeurs peuvent être des éléments quelconques.
Finalement, un Élément peut être aussi une liste Python, selon cette définition. Donc, vous avez une structure récursive, imbriquée, et même doublement (tuples dans des tuples).

Probablement la plupart de votre temps sera consommé par le débogage...

Envoyez vos solutions par mail, c'est votre exercice obligatoire, évalué (il y aura encore un). Cette fois l'évaluation sera plus sérieuse. Vous avez 12 jours, jusqu'au samedi soir, 31.10. Halloween. Si je reçois un message genre "désolé, mais je serai en retard, car l'Internet chez moi était défaillant, et mon binôme a eu une soudaine crise de pellicules sur son cuir chevelu", alors mon ordinateur vous enverra un rire diabolique, et vous subirez un sort pire que Voldemort.

Solutions (à venir)

Semaine suivante
Retour à l'index