Un peu sur les structures lexicales

"Tries" ou les arbres préfixés

Un trie est un concept inventé par Edward Fredkin, qui suggérait la prononciation [ˈtriː], car ceci venait de : information retrieval, mais corrompu par les successeurs : on prononce le mot : [ˈtraɪ], afin de ne pas le confondre avec tree.

Les tries sont des structures asociatives (comme une sorte de dictionnaires, sauf que l'on utilise la recherche arborescente, et non pas le hachage) facilitant la recherche de certains motifs dans les bases de données textuelles. Les tries sont utilisés dans plusieurs contextes, par ex. dans la complétion automatique des mots (sans doute vous l'avez vu dans vos téléphones portables, un dispositif très énervant !...), ou dans l'algorithme de césure automatique des mots (hyphenation), indispensable dans tous les éditeurs de texte. On en parlera encore.

Un trie est un arbre, dont un noeud typique n'a aucune valeur associé, mais les branches dont le nombre varie, sont étiquetées par des caractères. En suivant une branche depuis la racine, on assemble un mot. Les mots qui partagent le même préfixe, par ex. sapin, savoir, santé, ... partagent ce préfixe : sa, unique. Ainsi on peut économiser la mémoire de manière faible ou conséquente, mais seulement dans des cas favorables.

Voici un exemple un peu plus grand :

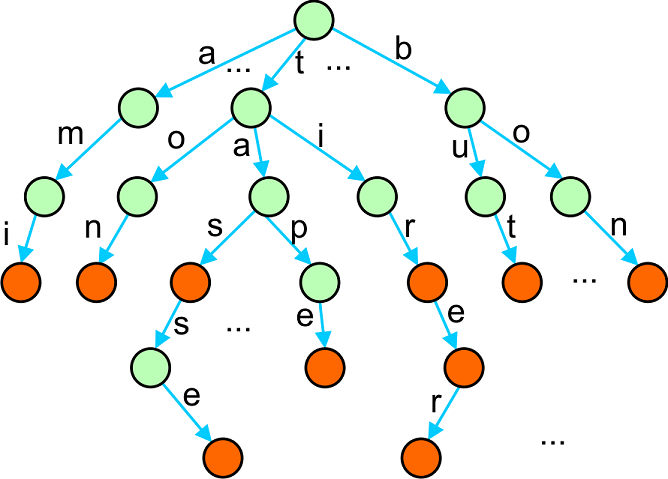Nous avons des mots comme : ami, ton, bon, but, tas, tasse, tir, tire et tirer. Les mots complets (les feuilles toujours, mais parfois quelques noeuds internes) sont marqués par une autre couleur.

On voit que la duplication des branches n'est pas supprimée, par ex. le mot basse ne peut partager le suffixe de tasse.

Un système primitif de complétion des mots peut utiliser un trie contenant des mots légaux. Quand l'utilisateur tape caractère après caractère, le module traverse l'arbre. À chaque instant il peut aller vers une feuille et proposer une continuation (ou plusieurs, par ex. classées par la probabilité, en accord avec une analyse préalable).

Prenons une liste de mots, et en construisons un trie. Dans Textes vous trouverez une liste_mots.txt contenant plusieurs mots français (avec leurs fréquences), un par ligne.

(Les fréquences ne sont pas utiles pour la construction des arbres).

Cette liste est assez longue, un peu trop, pour faire des petits tests. Pour vos expériences en TP ou chez vous, prenez par exemple seulement les mots qui commencent par "ta-" et ont moins de 7 lettres. Vous aurez 270 mots, un bon nombre pour faire des tests non-triviaux sans encombrer la mémoire.

Nous pourrons implémenter les tries de manière suivante :

  1. Un noeud est un objet Python, une classe spéciale. 
    class Trie(object):
    def __init__(self,...):
        ...
    def __repr__(self):
        ...
    ...
    2. Il possède un champ interne, un dictionnaire, dont les clés seront des caractères. Ce dictionnaire représente l'ensemble de branches, ainsi on peut implémenter facilement les arbres multi-branches. La valeur associée avec un caractère est le noeud suivant, la cible de la flèche correspondante.

  2. Un noeud contient un marqueur booléen, disons self.end, précisant que le mot se termine ici, alors il est True, sinon False. Ainsi on marque les feuilles, ce qui est un peu redondant, car la feuille est identifiée aussi par le fait que son dictionnaire des suffixes soit vide. Mais on marque les noeuds internes qui terminent un mot, par ex. si on ajoute "abc" et "abcdef", le noeud dont le dictionnaire possède 'd', est terminal aussi, car son préfixe "abc" est complet.

Il faudra écrire un programme qui assemble un trie en lisant plusieurs mots et en insérant chaque mot dans le trie, au début vide.

Ce sera une méthode .addword(self,wrd), qui peut insérer un mot dans un trie existant, et qui dûment marque sa fin par .end, feuille ou noeud interne.

Ensuite écrirons un programme qui trouve un mot complet dans le trie, s'il existe.

La construction des tries est un exemple paradigmatique d'algoritme récursif "progressif" (parfois appelé co-récursif). En deux mots : pour insérer un mot, on place le premier caractère, et on insère le reste.

La récursivité se termine quand le reste est vide, mais dans quelques circonstances dynamiques (remplacez le mot "insérer" par "engendrer" : émettre dans le réséau, etc.), on peut traiter des structures "formellement infinies", c'est-à-dire de longueur non-spécifiée.

Il est évident que dans la pratique toute opération doit se terminer).

Voici le paquetage. Comme il a été dit ci-dessus, un noeud : "Trie" possède deux champs internes, le marqueur booléen "end", et un dictionnaire de branches indexé par des caractères. 

class Trie(object):
    def __init__(self,wd="",end=False):
        self.br={}; self.end=end
        if wd!="": self.addword(wd)
    def __repr__(self): # Uniquement pour les tests
        br=self.br.__repr__()
        m='E,' if self.end else ""
        return "T["+m+br+"]"
On peut créer un Trie vide : z=Trie(), ou forcer tout de suite son initialisation avec un mot : z=Trie('unMot'). 
    def addword(self,wd):
        br=self.br
        if wd:
            c=wd[0]; rst=wd[1:] # Découpage essentiel
            if c not in br: br[c]=Trie() # Nouvelle branche
            br[c].addword(rst)
        else: self.end=True # Marqueur de la fin       
    def __getitem__(self,c):  # Objet émule une liste/dict.
        return self.br[c]
Si la suffixe d'un mot inséré existe (partiellement), on continue l'insertion en progressant le long de la séquence chaînée sans rien faire.

La suite est la construction d'une méthode .words(self) qui liste tous les mots dans le trie. On peut aussi construire une procédure qui efface un mot donné, s'il existe dans le trie ; cet exercice est moins important.

Les procédures / méthodes qui opèrent avec les arborescences, sont typiquement hautement récursives. Par ex. la stratégie d'insertion est basée sur le principe : traiter le premier caractère du mot, et ensuite insérer la queue restante.

Cependant attention, ceci est rudimentaire, peu économique, on peut faire mieux. Le compactage des tries, le ramassage des "chaînes solitaires", de manière à ce les branches ne soient plus indexées par des caractères individuels, mais par des chaînes plus longues [s'il n'y a pas d'ambiguïté] créé d'autres structures de données, les arbres des suffixes.

Ils sont fondamentaux dans les stratégies de recherche textuelle pour des raisons d'efficacité. Tous spécialistes les connaissent.

Ainsi pour l'exemple ci-dessus, le mot "ami", et les fragments "on" dans "bon" et "ton" constituent de tels suffixes. Dans de tels arbres tout noeud interne a au moins deux descendants.

La méthode .__getitem__(c) est un outil permettant d'écrire z[c] au lieu de z.br[c]. La méthode du rendu : .words() est compliquée à cause de la nécessité de traiter spécialement le cas des mots courts, qui se terminent avant la fin de la chaîne de liens, par ex. "abc" à l'intérieur de "abcdef". Elle est également récursive. On récupère tous les mots - suffixes, et on y ajoute le premier caractère à la tête. 

def words(self):
    br=self.br
    l=[]
    for c in br:
        w=br[c].words() # Les suffixes du mot en question
        if w==[]: x=[c] # Si vide
        else:
            x=[c+h for h in w] # Non vide. c à la tête
            if br[c].end: x+=[c] # Cas spécial ! 
        l+=x
    return l
Le cas spécial signifie que même si le mot le long de la branche parcourue continue, le noeud suivant est marqué comme terminal (feuille), donc il faut ajouter le mot composé de caractère c seul au résultat.

La méthode __repr__() sert à tester la structure de la construction : 

t=Trie("abc") 
t.addword("abcef")
t.addword("apext")
t.addword("new")
t.addword("next")
t.addword("ape")
rs=t.words()

print(t)
print(rs)
donne : 
T[{'a': T[{'b': T[{'c': T[E,{'e': T[{'f': T[E,{}]}]}]}], 
'p': T[{'e': T[E,{'x': T[{'t': T[E,{}]}]}]}]}], 
'n': T[{'e': T[{'x': T[{'t': T[E,{}]}], 'w': T[E,{}]}]}]}]

['abcef', 'abc', 'apext', 'ape', 'next', 'new']