Systèmes de Lindenmayer
Systèmes de Lindenmayer
Il s'agit d'une classe d'algorithmes récursifs de création, qui est basée sur une approche syntaxique. On construit une grammaire formelle; cette grammaire ne décrit (vraiment) pas des textes, comme des grammaires
ordinaires, ses instanciations sont des objets visuels, planaires ou volumiques.
Le concept a été inventé par un botanicien Néerlandais, Aristide Lindenmayer, et a évolué, déjà dans un contexte fort informatisé, grâce à Przemysław Prusinkiewicz, informaticien à Calgary, Canada. Ils ont écrit un livre "The Fractal Beauty of Plants"
(disponible en ligne et dans notre bibliothèque) qui montre de
très nombreux exemples.
F -> F+F--F+FLa grammaire – on peut le dire – établit les règles du développement « génétique » de l'objet. Élaborons un exemple complet basé sur les éléments introduits ci-dessus. Trois symboles, "F", "+" et "-", et la seule règle ci dessus, doivent être complétés par la précicion concernant la longueur du pas (largement conventionnel, question d'échelle), et l'angle de rotation de la plume, par convention historique souvent décrit comme l'inverse de la fraction de 360°. Ici Angle=6, c'est-à-dire : 60°.
La règle ci-dessus est hautement récursive ! (et il n'y a pas d'alternatives permettant de l'arrêter).
Si on appliquait cette transformation "jusqu'au bout", on aurait une structure infinie. Considérons donc le remplacement spécifié par la règle, comme une règle d'évolution du système, un pas dans le temps. Si le 'F' initial est une ligne horizontale, voici les instances récursives des premiers niveaux, 1, 2, et 4, si le niveau 0, l'axiome, est F.
Ce système décrit (en profondeur infinie) une courbe fractale connue sous le nom de courbe de Von Koch, connue aussi comme le "flocon de neige fractal".
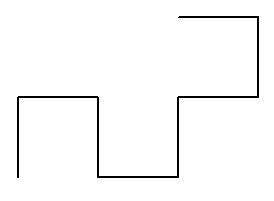Voici les règles (non-uniques, d'autres similaires existent), et les échantillons de profondeur 3, 8 et 12. L'angle vaut 90°, et l'axiome est FX.
X -> X-YF Y -> FX+Y
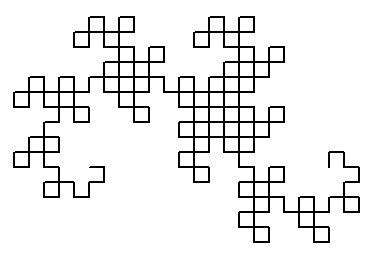
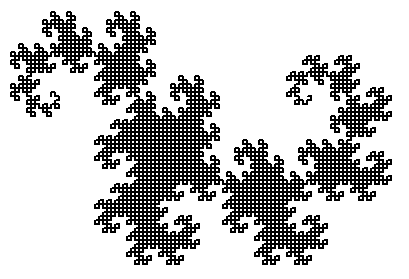
Cependant, si les actions graphiques se réduisent au traçage, on obtient forcément une courbe, même exotique. Nous pourrons tracer aussi des arbres, et en fait : des graphes quelconques. Si nous ajoutons au système des nouveaux symboles, traditionnellement '[' et ']', on pourra dessiner des objets comme à droite.
F -> FF-[-F+F+F]+[+F-F-F]Attention, une itération multiplie la longueur de la chaîne résultante par 8. Tout ceci suffit pour faire simples expériences. Mais l'Internet est plein de paquetages pour les systèmes de Lindenmayer ! En couleurs, 3D, extra éléments (le feuillage d'un arbre, les pétales des fleurs), règles stochastiques (aléatoires), avec des grammaires contextuelles, etc.
turtle. On peut le faire beaucoup mieux. La discussion ci-dessous ne couvre pas les détails de la gestion de la "tortue". Le système est une classe Python :
from turtle import *
class Linden(object):
def __init__(self,axiom,stp,ang,rules):
self.ax=axiom # Chaîne de départ
self.rules=rules # Liste de règles
self.stp=stp; self.ang=ang; # pas et angle
self.wd=2; self.col=(0,0,0) # largeur et couleur
self.cur=self.ax
self.prim={'+':self.lf,'-':self.rt,'F':self.fd,
'[':self.save,']':self.rstr}
self.stak=[]; self.dct={}
Les primitives graphiques du système sont des méthodes associées aux symboles, comme décrit ci-dessus. On peut facilement modifier ce dictionnaire, l'enrichir, etc. stak est la pile de sauvegardes d'état, et dct - le dictionnaire de règles. Ces dernières sont des listes de 2-tuples, par ex. regdr=[('X','X-YF'), ('Y','FX+Y')]. Elles sont placées dans le dictionnaire :
for cr in self.rules:
c,r = cr; self.dct[c]=r
self.reset()
Quelques procédures peuvent faciliter la gestion de la tortue de l'intérieur du système :
def color(self,col):
self.col=col; color(self.col)
def reset(self,x=0,y=0,ang=0,wid=2):
penup(); goto(x,y); seth(ang); # set heading
self.wd=wid; width(self.wd)
pendown()
speed(0); color(self.col); ht(); # hide turtle
Passons aux méthodes de traçage. On peut y ajouter (avec les symboles) le recul de la tortue, la modif. dynamique de l'angle ou du déplacement, changement de couleur, etc.
Ceci compliquera le parsing des chaînes, mais avec les expressions régulières on peut introduire des symboles composites, comme @0.85, etc. (Ceci est une variante de la construction qui rétrécit le pas élémentaire de la plume.)
def fd(self):
forward(self.stp)
def lf(self):
left(self.ang)
def rt(self):
right(self.ang)
def vid(self): pass
def save(self):
p=(xcor(),ycor(),heading())
self.stak.append(p)
def rstr(self):
(x,y,hd)=self.stak.pop()
penup()
setx(x); sety(y); seth(hd)
pendown()
Voici les méthodes de traçage, et d'évolution du système (remplacement des chaînes).
def draw(self):
for c in self.cur:
f=self.prim.get(c,self.vid)()
def evol1(self):
res=""
for c in self.cur:
st=self.dct.get(c,c)
res+=st
self.cur=res
def evol(self,n=1):
for k in range(n): self.evol1()
Voici la courbe de von Koch :
regk=[('F','F+F--F+F')]
koch=Linden('F',10,60,regk)
koch.reset(x=-400,y=-100) # pour ne pas sortir de l'espace
koch.evol(4); koch.draw();
[('F',''),('X','----F!X!++++++++F!X!----')]
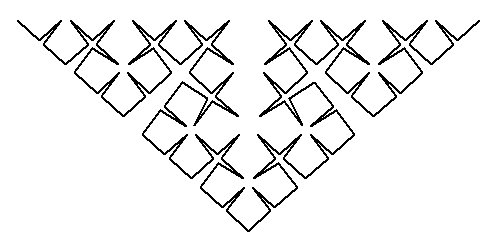L'angle est 360°/34, et l'axiome est 'FX'.
Constatez la présence du symbole '!'. Traditionnellement ceci est l'inversion dans le miroir des commandes qui suivent. '+' agit comme '-' et vice-versa, c'est-à-dire, '+' tourne à droite.
Implémentez ce mécanisme. Penser à sauvegarder l'orientation, le sens des commandes '+-' sur la pile par '[' !
Dans le cas Cesàro, ceci n'est pas important, mais en général, si.
Un autre exercice.
Le "tapis de Sierpiński". (Normalement cette forme, une "courbe qui remplit l'espace" est dessinée avec des méthodes plus efficaces, mais l'approche grammaticale est universelle). Il faudra implémenter une méthode triviale, 'G', qui déplace la tortue exactement comme 'F', mais sans rien tracer (la plume est soulevée). Les règles sont :
('F','F+F-F-F-G+F+F+F-F'),('G','GGG')
L'angle est de 90°, et l'axiome est 'F'. {5}
|
|