Traitement élémentaire des textes
Codage
Puisque on s'occupera pour l'instant de la structure superficielle des textes (pas de règles morphologiques, seulement les aspects probabilistes, la répartition des lettres et des n-grammes), il faut établir une relation disciplinée entre les "lettres" – en tant qu'unités lexicales d'un texte, et ce que "voit" l'ordinateur, les octets, les nombres. Cette relation n'est nullement triviale, et souvent dérangeante, à cause d'erreurs historiques provoquées par la domination du code ASCII dans le monde informatique, bon seulement pour les textes en Anglais (et pas tous).
Mais nous voulons travailler dans un cadre plurilingue, et c'est sérieux.
À l'heure actuelle plusieurs systèmes de codage coexistent, les textes sur lesquels nous travaillerons sont hétérogènes, et plusieurs logiciels traitent les caractères non-ASCII de manière variée. Il faut s'habituer, savoir reconnaître les causes de défaillance de codage quand elles se produisent, et savoir les corriger. Il vous faudra (peut-être) travailler sur la configuration de vos systèmes, vos éditeurs, vos navigateurs Web, et un jour : vos serveurs.
La pagaille est difficile à éviter... Les interfaces Python comme Idle, Spyder, etc. se comportent également de manière différente (surtout sous Windows).
Python en tant que tel nous aide un peu, les données textuelles sont "abstraites" (lire : Unicode). Quand on tape : a="é"; b="żółć"; c="tão"; d="привет", on créé 4 chaînes, de 1, 4, 3 et 5 caractères Unicode. Dans une fenêtre raisonnable (Idle, console IPython... mais NON PAS la console Windows !) ils s'affichent comme ci-dessus.
Mais si on les transforme en octets, tout depend de schéma de codage, par ex. :
>>> bytes('é','cp1252')
b'\xe9' # Occidental ; 1 octet
>>> bytes('é','utf-8')
b'\xc3\xa9'
Cependant les caractères cyrilliques ou autres n'admettent pas le codage "ancien" :
>>> bytes('ż','utf-8')
b'\xc5\xbc'
>>> bytes('и','utf-8')
b'\xd0\xb8'
>>> bytes('ż','cp1252')
Traceback (most recent call last):
File "", line 1, in
bytes('ż','cp1252')
File "C:\Anaconda3\lib\encodings\cp1252.py", line 12, in
encode return codecs.charmap_encode(input,errors,
encoding_table)
UnicodeEncodeError: 'charmap' codec can't encode character
'\u017c' in position 0: character maps to <undefined>
Nous allons utiliser surtout le codage UTF-8 (voir aussi cette liste), et si besoin convertir tous les textes vers cette norme. Les caractères sont codés comme des séquences entre 1 et 4 octets, ce qui permet de coder toutes les entités Unicode, et donc presque toutes les langues. La norme est compatible avec le vieux ASCII, les caractères latins non-accentués, codés en un octet : 7 bits entre 0 et 127. Les caractères français accentués (et 'ç') en code Occidental (Windows ou ISO-Latin-1) occupent 1 octet, le code est > 128. Les caractères dans les langues européennes codés en UTF-8 prennent d'habitude 2 octets et le mauvais décodage donne des résultats reconnaissables. Le texte lu ci-dessous est codé en UTF-8, mais les interfaces Python qui par défaut utilisent ISO, donnent :
fl=open("../Textes/declar_dh.txt","r")
for x in fl: print(x)
...
Tous les êtres humains naissent libres et égaux en dignité
et en droits. Ils sont doués de raison et de conscience
et doivent agir les uns envers les autres dans un esprit de
fraternité.
Afin d'obtenir le résultat correct, on doit lancer :
fl=open("../Textes/declar_dh.txt","r",encoding="utf-8").
... et le HTML?
Le codage des caractères internationaux dans des documents Web balisés (et donc structurés, avec des entêtes, et d'autres méta-informations) est assez flexible. Les textes avec des caractères internationaux en UTF-8 demandent la préfixation :
<html xmlns=... lang="fr">
<meta http-equiv="content-type"
content="text/xml; charset=UTF-8" />
On peut insérer les caractères par leur codes, par ex. le caractère "ê", Unicode : U+00EA possède le code HTML ê . Le z dur Polonais : "ż" est : ż, etc.
Unicode
Unicode, (ou l'essentiel de la norme ISO 10646), développé depuis 1991, est un standard contenant plus de 110 000 entités lexicales en une centaine d'écritures, avec des précisions concernant les relations entre minuscules et majuscules – où applicable –, de la direction de l'écriture, du tri, des variantes, etc. L'espace Unicode dispose de 1 114 112 positions de code (code points) de 0 à 10FFFF hex, mais moins d'un quart est utilisé actuellement.
Unicode n'est pas une "liste de caractères" numérotée. Les entités dedans décrivent l'accentuation (il y a une relation entre "é" et "e" et entre "ś" et "s" ; ceci est essentiel pour l'affichage des textes nationaux sur une interface restreinte), chaque caractère a un long nom descriptif, et le standard parle aussi (partiellement) des règles de ponctuation. Il est structuré en couches, voici une description incomplète.
-
Caractères abstraits, "symboliques", par ex. "Î" est connu comme
LATIN CAPITAL LETTER I WITH CIRCUMFLEX.
-
Codage conceptuel, "points de code". Ceci n'est pas la représentation dans la mémoire, mais un nombre entier pour l'identification. Ensemble les points de code constituent son espace, divisé en 17 zones de $2^{16}$ entités. Le point de code est noté : U+XXXX ... où XXXX est en hexadécimal, et sa longueur dépend de la zone (plan) : 4, 5 ou 6 chiffres.
-
Formalisme de codage. C'est la représentation physique, dans la mémoire et les documents. Cela peut occuper 1, 2, ou 4 octets. Il existe plusieurs variantes de ce codage, l'UTF-8 est l'un d'eux.
Ensuite vont : le schéma de sérialisation (qui spécifie l'ordre des octets), et la dernière couche s'occupe du chiffrement et de compression standardisées.
Format de transformation UTF-8
Les schémas UTF-8, avec UTF-16 et UTF-32 sont des formalismés préférés de représentation des caractères Unicode dans des documents. Ils sont de taille variable, et compatibles de manière économique avec les caractères occidentaux (et surtout avec ASCII ; un seul octet). Cependant, puisque on peut avoir 1, 2 jusqu'à 4, afin de couper une sous-chaîne dans un document, il faut faire des calculs, a priori on ne voit pas sur quel octet la chaîne commence. Ceci ralentit le traitement.
L'UTF-8 est utilisé par 80% des sites Web, et contrairement à Windows, c'est un standard courant sous Linux. Il a été inventé en 1992. L'IETF (Internet Engineering Task Force) exige à ce que tous les nouveaux protocoles d'échange sur l'Internet, utilisent ce codage par défaut (pour les anciens c'est plus délicat, questions de compatibilité). De toute façon, tous les navigateurs et tous les logiciels de mail acceptent ce codage.
Votre seul problème sera éventuellement votre éditeur de texte, et le traitement du texte vu comme une séquence binaire, sans interprétation. Alors vous serez obligés de faire beaucoup de calculs ; il est préférable de travailler sur la couche symbolique, ce qui en Python est facile...
Traitement statistique des textes
Fréquence de lettres
La modélisation statistique des énoncés commence par cela. Nous avons un peu de théorie de probabilité (assez élémentaire) à discuter, mais cela viendra après notre première expérience pratique en Python.
Nous voulons calculer le nombre (plus tard normalisé, divisé par le nombre total) de caractères dans une chaîne, lue depuis un document sur le disque. Nous ne voulons pas nous occuper de codage numérique des caractères. Python nous offre la possibilité d'utiliser les caractères (chaînes ; en Python un caractère est représenté comme une chaîne de longueur 1 sur le plan abstrait : nous savons que les caractères non-ASCII prendront plusieurs octets) comme indices / clés dans les dictionnaires. Les instructions d={}; d['é']=17 sont légitimes.
L'algorithme en question consiste à définir un dictionnaire vide, et de parcourir la chaîne ; pour chaque nouveau caractère on place 1 dans l'élément indexé par ce caractère, et s'il a été déjà vu, on incrémente la valeur. Les caractères non-vus seront totalement absents. Parfois ceci pose des problèmes, et il faut commencer par l'initialisation du dictionnaire avec zéros, avec les clés récupérées depuis l'alphabet complet. Il faut alors le connaître...
On lira le texte de la Déclaration universelle des droits de l'homme
fg = open("../Textes/declar_dh.txt","r",encoding="utf-8")
sg = fg.read()
Cependant, si on affiche cette chaîne par l'expression sg tout court, on obtiendra (sans coupures de lignes !) :
"\ufeffDéclaration universelle des droits de l'homme\n\n
Paris, le 10 décembre 1948\n\nPréambule\n\nConsidérant que
la reconnaissance de la dignité inhérente à tous les membres
de la famille humaine et de leurs droits égaux et
inaliénables constitue le fondement de la liberté, de la
justice et de la paix dans le ..."
ce qui est différent du résultat de : print(sg) :
Déclaration universelle des droits de l'homme
Paris, le 10 décembre 1948
Préambule
Considérant que la reconnaissance de la dignité inhérente
à tous les membres de la famille humaine et de leurs droits
égaux et inaliénables constitue le fondement ..."
Quelques commentaires seraient utiles.
-
La représentation visuelle, mais "interne" des chaînes (la méthode __repr__ des chaînes) n'interprète pas les fins de ligne.
-
Le premier caractère \ufeff est un symbole Unicode connu comme BOM : Byte Order Mark qui n'a pas de sens direct dans l'UTF-8, mais marque le document comme codée de cette manière. Ceci est indispensable pour quelques navigateurs Web, mais en général son usage est déconseillé.
Le code qui calcule les fréquences peut être :
def frq(s):
dct={}; n=0 # total
for c in s:
if c in dct: dct[c]+=1
else: dct[c]=1
n+=1
for c in dct: dct[c]/=n
return dct
d=frq(sg)
Le dictionnaire aura le contenu :
{'ê': 0.0019008264462809918,
'2': 0.0021487603305785125,
';': 0.0004958677685950413,
'ù': 0.00033057851239669424,
'h': 0.0038016528925619835,
'O': 8.264462809917356e-05,
'p': 0.02,
'6': 0.00024793388429752067,
...
Ceci n'est pas très lisible. Il nous sera utile de trier cette collection selon la fréquence de caractères, décroissante. Ensuite, nous dessinons la courbe résultante, à l'aide du paquetage Matplotlib (et son module pylab). Comme vous voyez, nous profitons de cet exercice pour vous apprendre quelques techniques de programmation Python de base, utiles dans ce domaine. Voici le tri :
sl=sorted(list(d.items()),key=lambda x:x[1],reverse=True)
ce qui donne :
[(' ', 0.15652892561983472), ('e', 0.11173553719008264),
('t', 0.06900826446280992), ('i', 0.06520661157024793),
('n', 0.06198347107438017), ('s', 0.06),
('a', 0.05545454545454546), ('r', 0.05190082644628099),
('o', 0.05107438016528926), ('l', 0.04462809917355372),
('u', 0.040991735537190085),('d', 0.03553719008264463),
('c', 0.027107438016528925),('é', 0.02140495867768595),
('p', 0.02), ('m', 0.01785123966942149),
('\n', 0.01347107438016529),(',', 0.009834710743801652),
('.', 0.00768595041322314), ...]
et encore quelques commentaires s'imposent.
-
Un dictionnaire n'admet aucun ordre, nous l'avons converti en liste de tuples (clé,valeur), et trié le résultat selon le second élément, en décroissance. Il est dans votre intérêt avoir sous la main la documentation de Python...
-
Le résultat est tel qu'il est, mais il n'est pas "propre" : le programme fait la différence entre les majuscules et les minuscules, compte la fréquence des caractères de ponctuation (et du BOM), donc si nous voulions traiter statistiquement les lettres dans une langue, il faudrait effectuer un pré-traitement des données, éliminer les "miettes".
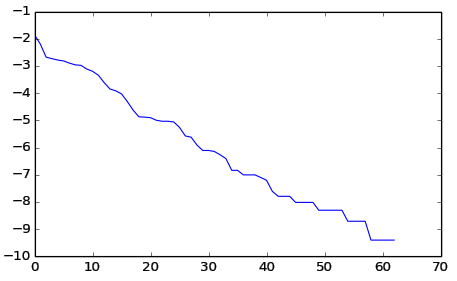 Voici le graphique :
Voici le graphique :
from pylab import *
fr=[log(x) for (c,x) in sl]
plot(fr); show()
On dessine seulement les fréquences, en oubliant les clés.
Nous avons opté pour l'échelle verticale logarithmique, car la linéarité du résultat (donc, le caractère approximativement exponentiel de la courbe) est plus lisible. Est-ce que ce résultat est pertinent et "correct"?
La statistique des fréquences dans la langue française commence (en décroissance) par : "esaitnrulodcpmévq ...". Nous avons obtenu : " etinsaroludcépm\n ...", ce qui n'est pas exact. Mais la ponctuation change les proportions, et la séparation entre les minuscules et les majuscules aussi.
La répartition fréquentielle des lettres "en français", est une notion ambiguë. Tout dépend de l'échantillon. Un texte avec des instructions (par ex. un manuel), qui s'adresse au lecteur par "vous" aura plus d'occurrences de "z" ("branchez" ...) qu'un texte neutre.
Les fréquences dans un texte, et les fréquences dans des mots tirés d'un dictionnaire sont également différentes ! Dans un dictionnaire il y a peu de pluriel ; dans le texte la fréquence de "s" sera plus grande.
Une telle analyse permet de manière approximative résoudre le problème de "cryptage bête", où chaque caractère est remplacé par un autre, selon une liste de correspondances. On identifie facilement les caractères les plus fréquents. Ce sera un exercice en TP.
Nous voudrons synthétiser un texte artificiel, qui "simule" un texte réel. Mais la fréquence des caractères individuels ne suffit pas, il faut tenir compte des corrélations entre les caractères voisins. En Tchèque (un peu en Polonais) on trouve des mots avec plusieurs consonnes consécutives, par ex. une phrase tchèque comme "Strč prst skrz krk" peut facilement zblbnout le lecteur... (Cherchez la traduction vous-mêmes...). En Français ceci n'est pas possible, en Italien encore moins...
Quelques éléments de la théorie de probabilité
Probabilités conditionnelles
Un peu de théorie (pas si théorique), indispensable pour la modélisation statistique des structures linguistiques... Nous allons traiter ici des distributions multi-dimensionnelles, qui sur le plan abstrait peuvent décrire plusieurs espaces de données : fréquence des lettres, fréquences des mots, ou des données qui n'ont rien à voir avec TAL, mais vous seront utiles dans d'autres branches d'Informatique. On parlera des lettres uniquement pour avoir un modèle concret à travailler avec, mais nous ferons en TP d'autres exemples.
L'apparition d'une combinaison concrète de lettres contiguës dans l'ordre sera caractérisée par la probabilité jointe, multi-dimensionnelle $p(l_1, l_2,\ldots,l_n)$. Cette combinaison sera appelée : n-gramme (bigramme, trigramme, etc.) Dans le texte "Belle marquise" on trouve les trigrammes : Bel, ell, lle, le˽, e˽m, ˽ma, mar, ... etc.
La construction du tableau des probabilités des n-grammes procède selon les mêmes principes que la construction des fréquences des lettres. Pour un texte t on sépare dans une boucle t[k:k+n], on l'utilise comme une clé dans un dictionnaire, et on incrémente la valeur de cet élément.
Cependant, pour la génération d'un texte qui respecte la distribution des n-grammes, rien n'est évident. Supposons que l'on travaille sur les 3-grammes. Dans un texte de 4 lettres les trois premières doivent être choisies selon la probabilité voulue, mais les trois dernières aussi, et une partie de cette donnée est déjà là. Il faut procéder d'une autre façon, séquentielle.
Afin d'engendrer un digramme, par ex. la séquence "es" avec la probabilité correcte, nous allons engendrer "e" avec la probabilité (fréquence) appropriée pour cet 1-gramme, et ensuite la lettre "s" selon la probabilité conditionnelle : la probabilité de "s" sachant que "e" a déjà été choisi.
Cette probabilité conditionnelle sera notée : $p(l_2|l_1)$. La cohérence exige que la formule ci-dessous soit respectée.
$$ p(l_1,l_2) = p(l_1) \cdot p(l_2|l_1)\,.$$
Ceci suggère simplement que le calcul de la probabilité conditionnelle peut simplement utiliser : $p(l_2|l_1) = p(l_1,l_2)/p(l_1)$. En général :
$$
p(l_1,l_2,\ldots,l_n) = p(l_1) p(l_2|l_1) p(l_3|l_1 l_2) \cdots p(l_n|l_1 l_2 \ldots l_{n-1})\,.
$$
Pour le codage d'un texte synthétique qui respecte les n-grammes, il faut s'assurer que les probabilités de tous les m-grammes pour $m < n$ soient également correctes. Il faut savoir faire plusieurs choses :
-
Calculer depuis le texte-échantillon l'ensemble complet des probabilités 1-, 2-, ... (n-1)-, et n-dimensionnelles des multi-grammes.
-
Reconstruire toutes les probabilités conditionnelles pertinentes.
-
Coder un générateur aléatoire en accord avec les probabilités en question. Ceci sera discuté dans la section suivante.
-
Finalement, synthétiser le texte. Nous allons travailler au niveau des lettres, mais aussi des mots. Un discours réel sera utilisé pour la construction d'un texte synthétique. De telles expériences servent pour la validation/tests des algorithmes qui doivent respecter certaines propriétés statistiques.
Génération de nombres aléatoires
La création des nombres aléatoires réels ou entiers dans un intervalle, et aussi des vecteurs aléatoires, ou des fonctions aléatoires (signaux bruités) est essentiel dans plusieurs branches d'informatique (automatique, physique, et mathématiques appliquées en général). Ceci constitue une introduction très compacte et incomplète. Commençons par la génération considéré élémentaire, primitive, normalement disponible dans les librairies standard de tous les langages de programmation populaires.
Nous n'allons pas discuter les algorithmes de base pour engendrer les nombres aléatoires de distribution uniforme dans un intervalle, mais quelques mots, afin d'éviter des malentendus peuvent être utiles.
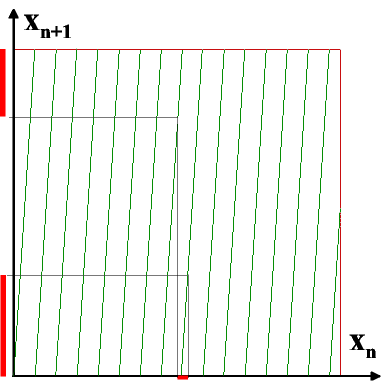 La première vérité est : les générateurs aléatoires n'ont rien d'aléatoire ! La procédure de génération est (sauf des cas exceptionnels, spéciaux) parfaitement déterministe, afin que l'on puisse répéter les mêmes séquences "aléatoires" et tester des algorithmes statistiques de manière répétable. La technique classique est basée sur l'usage des fonctions très instables : des fonctions telles qu'une très petite différence des arguments, produit une grande (arbitraire) différence des résultats.
Imaginez la fonction $f(x) = R \cdot x \pmod 1$, où $x$ est une valeur entre 0 et 1, et $R$ un grand nombre. (Ici : quelques dizaines, mais dans la pratique – plusieurs millions voire plus). Voici le graphique de cette fonction. Elle est très instable :
La première vérité est : les générateurs aléatoires n'ont rien d'aléatoire ! La procédure de génération est (sauf des cas exceptionnels, spéciaux) parfaitement déterministe, afin que l'on puisse répéter les mêmes séquences "aléatoires" et tester des algorithmes statistiques de manière répétable. La technique classique est basée sur l'usage des fonctions très instables : des fonctions telles qu'une très petite différence des arguments, produit une grande (arbitraire) différence des résultats.
Imaginez la fonction $f(x) = R \cdot x \pmod 1$, où $x$ est une valeur entre 0 et 1, et $R$ un grand nombre. (Ici : quelques dizaines, mais dans la pratique – plusieurs millions voire plus). Voici le graphique de cette fonction. Elle est très instable :
ff(0.3400000) $\to$ 0.22000000067055225
ff(0.3400001) $\to$ 0.51815330050885677
Ceci constitue l'algorithme dit congruentiel de génération des distributions aléatoires uniformes.
Dans la pratique on n'utilise pas les nombres réels, car leur précision dépend du système, parfois du langage, mais le comportement des fonctions entières est similaire, la fonction $r(K) = A \cdot K + C \pmod M$, où $M$ est un nombre très grand, dépendant de la machine ; par ex. $2^{32} - 1$, $K$ et les autres, appartiennent à l'intervalle $0$ – $M-1$. En divisant le résultat par $M$ on obtient un nombre réel entre 0 et 1.
D'autres algorithmes numériquement meilleurs existent, mais ne seront pas discutés ici. Le module standard random offre plusieurs fonctions. Par ex. random() retourne un nombre pseudo-aléatoire entre 0 et 1. randint(a, b) - un nombre entier $N$ : $a \le N \le b$. La fonction choice(seq) retourne un élément de la séquence-argument, avec la probabilité uniforme.
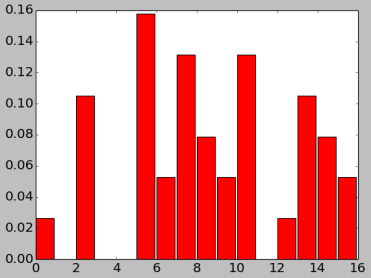 Mais pour la génération des n-grammes dont la distribution est non-uniforme il faut des générateurs plus compliqués. Voici une méthode universelle, vous n'aurez pas besoin de la coder. L'idée est la suivante.
$p[k]$ est un tableau (prob. discrète) de fréquences (normalisées, leur somme vaut 1). Nous voulons construire un algorithme qui engendre des nombres (ici) entre 0 et 15 avec les mêmes probabilités.
Mais pour la génération des n-grammes dont la distribution est non-uniforme il faut des générateurs plus compliqués. Voici une méthode universelle, vous n'aurez pas besoin de la coder. L'idée est la suivante.
$p[k]$ est un tableau (prob. discrète) de fréquences (normalisées, leur somme vaut 1). Nous voulons construire un algorithme qui engendre des nombres (ici) entre 0 et 15 avec les mêmes probabilités.
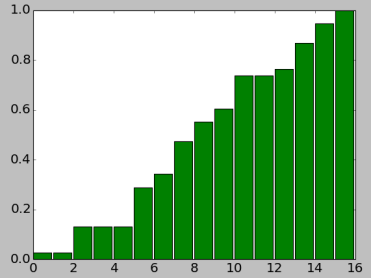 On "jette un projectile" dans la zone rouge du rectangle du graphique, et la colonne qui sort de cette opération, est le résultat. On n'aura jamais 1, 3, 4, ni 11, et 5 est la valeur la plus probable. L'implémentation commence par la construction d'un tableau auxiliaire, de la distribution cumulative. $d[k] = \sum_{j=0}^k p[k]$.
Puisque les valeurs dans $p$ sont non-négatives, c'est une séquence monotone, $d[i+1] \ge d[i]$. Voici la génération :
On "jette un projectile" dans la zone rouge du rectangle du graphique, et la colonne qui sort de cette opération, est le résultat. On n'aura jamais 1, 3, 4, ni 11, et 5 est la valeur la plus probable. L'implémentation commence par la construction d'un tableau auxiliaire, de la distribution cumulative. $d[k] = \sum_{j=0}^k p[k]$.
Puisque les valeurs dans $p$ sont non-négatives, c'est une séquence monotone, $d[i+1] \ge d[i]$. Voici la génération :
-
On tire un nombre aléatoire entre 0 et 1. On le considère comme la hauteur, choisie sur l'axe des ordonnées (verticale).
-
On trace une ligne horizontale, jusqu'à l'intersection avec une colonne verte. Cette colonne est retournée comme le résultat.
-
On voit que le choix plus probable est quand le segment accessible par cette manipulation est le plus grand. Les zéros dans $p$ produisent des colonnes $d$ cachées derrière les autres ; elles ne seront jamais trouvées.
Voici le programme et son test.
from pylab import *
seed(5427462) # Init. random
freq=[1,0,4,0,0,6,2,5,3,2,5,0,1,4,3,2]
def gener(freq):
s=sum(freq); p=[x/s for x in freq] # normalis.
d=cumsum(p) # Sommes partielles ; distr. cumul.
def ff():
r=random()
k=0
while r>d[k]: k+=1
return k
return ff
tst=gener(freq)
seq=array([tst() for j in range(100000)])
hist(seq,bins=range(17)); show()
Notez la technique de programmation "indirecte". La fonction gener accepte comme paramètre les probabilités (fréquences), et construit et exporte une fonction interne, qui n'a plus de paramètres.
$\definecolor{gre}{RGB}{0,100,0}$
Digression très importante : théorème de Bayes
Ce sujet est largement indépendant du TAL, mais exploité en permanence ici, en IA, dans l'analyse des données visant à confirmer une hypothèse, dans les estimations concernant les populations dont on connaît des échantillons. On dit que pour la statistique le théorème de Bayes (Thomas Bayes, 1701 – 1761) est comme le théorème de Pythagore en géométrie... Sa formulation est la conséquence directe de la loi des probabilités conditionnelles. Parlons désormais d'"événements" qui peuvent - ou non - avoir lieu : A, B, C... [Par ex. l'occurrence des lettres/mots dans un texte ; apparition d'un document dans une langue précise, etc. D'autres exemples suivront]. Voici sa formulation mathématique :
$$\color{gre}p(A|B) = \frac{p(B|A)\cdot p(A)}{p(B)}\,.$$
L'exemple le plus classique : de quelle urne vient la boule?... Ayant deux urnes, dont la première a 30 urnes blanches et 10 noires, et la seconde : 20 de chaque couleur, on tire aléatoirement une boule d'une urne choisie également au hasard. La boule est blanche. De quelle urne elle vient (statistiquement)? Voici le raisonnement qui "renverse les prémisses et l'hypothèse".
Nous avons les événéments : couleur, et numéro de l'urne : B, N ; U1, U2. L'énoncé du problème affirme que $p(B|U_1)=0.75$, $p(B|U_2)=0.5$. Les autres probabilités sont facilement obtenus, $p(N|U_1)=1-p(B|U_1)$, car ces événéments sont contradictoires. Nous cherchons $p(U_1|B)$.
Bayes dit que $p(U_1|B) = p(B|U_1)\cdot p(U_1)/p(B)$. Mais les tirages de deux urnes sont complémentaires, $p(B) = p(B|U_1)\cdot p(U_1) + p(B|U_2)\cdot p(U_2)$. On a $p(B)$ : $0.75 \cdot 0.5 + 0.5 \cdot 0.5 = 0.625$. La réponse est $0.375/0.625 = 0.6$.
Supposons qu'un test de dopage a la sensitivité 99%, et la spécificité 99%, c'est à dire qu'il donne pour les dopés (D) le résultat positif (+) en 99% des cas, et en 99% pour les non-dopés (N) le résultat sera négatif (-).
Supposons que 0.5% membres du groupe testé se dopent. Une personne choisie aléatoirement engendre le résultat positif. Quelles sont les chances qu'elle se dope? Les données suggèrent que très grandes, que le test est fiable. Cependant le théorème de Bayes dit que $p(D|+)$ vaut :
$$\frac{p(+|D)p(D)}{p(+|D)p(D) + p(+|N)p(N)}=\frac{0.99 \cdot 0.005}{0.99 \cdot 0.005 + 0.01 \cdot 0.995} = 0.3322$$
Pas si fiable... Analysez pourquoi !. Pour les hypothèses dans le domaine linguistique les résultats non-concluants sont encore plus fréquents. Fin de digression.
 La première vérité est : les générateurs aléatoires n'ont rien d'aléatoire ! La procédure de génération est (sauf des cas exceptionnels, spéciaux) parfaitement déterministe, afin que l'on puisse répéter les mêmes séquences "aléatoires" et tester des algorithmes statistiques de manière répétable. La technique classique est basée sur l'usage des fonctions très instables : des fonctions telles qu'une très petite différence des arguments, produit une grande (arbitraire) différence des résultats.
Imaginez la fonction $f(x) = R \cdot x \pmod 1$, où $x$ est une valeur entre 0 et 1, et $R$ un grand nombre. (Ici : quelques dizaines, mais dans la pratique – plusieurs millions voire plus). Voici le graphique de cette fonction. Elle est très instable :
La première vérité est : les générateurs aléatoires n'ont rien d'aléatoire ! La procédure de génération est (sauf des cas exceptionnels, spéciaux) parfaitement déterministe, afin que l'on puisse répéter les mêmes séquences "aléatoires" et tester des algorithmes statistiques de manière répétable. La technique classique est basée sur l'usage des fonctions très instables : des fonctions telles qu'une très petite différence des arguments, produit une grande (arbitraire) différence des résultats.
Imaginez la fonction $f(x) = R \cdot x \pmod 1$, où $x$ est une valeur entre 0 et 1, et $R$ un grand nombre. (Ici : quelques dizaines, mais dans la pratique – plusieurs millions voire plus). Voici le graphique de cette fonction. Elle est très instable :
 Mais pour la génération des n-grammes dont la distribution est non-uniforme il faut des générateurs plus compliqués. Voici une méthode universelle, vous n'aurez pas besoin de la coder. L'idée est la suivante.
$p[k]$ est un tableau (prob. discrète) de fréquences (normalisées, leur somme vaut 1). Nous voulons construire un algorithme qui engendre des nombres (ici) entre 0 et 15 avec les mêmes probabilités.
Mais pour la génération des n-grammes dont la distribution est non-uniforme il faut des générateurs plus compliqués. Voici une méthode universelle, vous n'aurez pas besoin de la coder. L'idée est la suivante.
$p[k]$ est un tableau (prob. discrète) de fréquences (normalisées, leur somme vaut 1). Nous voulons construire un algorithme qui engendre des nombres (ici) entre 0 et 15 avec les mêmes probabilités.
 On "jette un projectile" dans la zone rouge du rectangle du graphique, et la colonne qui sort de cette opération, est le résultat. On n'aura jamais 1, 3, 4, ni 11, et 5 est la valeur la plus probable. L'implémentation commence par la construction d'un tableau auxiliaire, de la distribution cumulative. $d[k] = \sum_{j=0}^k p[k]$.
Puisque les valeurs dans $p$ sont non-négatives, c'est une séquence monotone, $d[i+1] \ge d[i]$. Voici la génération :
On "jette un projectile" dans la zone rouge du rectangle du graphique, et la colonne qui sort de cette opération, est le résultat. On n'aura jamais 1, 3, 4, ni 11, et 5 est la valeur la plus probable. L'implémentation commence par la construction d'un tableau auxiliaire, de la distribution cumulative. $d[k] = \sum_{j=0}^k p[k]$.
Puisque les valeurs dans $p$ sont non-négatives, c'est une séquence monotone, $d[i+1] \ge d[i]$. Voici la génération :
 Voici le graphique :
Voici le graphique :