Processus quantiques et logique linéaire

Disclaimer : cet exposé appartient plutôt à la philosophie qu'à l'informatique...

Vous êtes encore là?

Notre objectif était d'implémenter les calculs quantiques sur l'ordinateur de manière "honnête" - de la perspective d'un physicien qui respecte la Nature. (Les informaticiens de pur jus ne le font pas, car leur "monde" ce sont des structures conceptuelles, leurs modèles, dont EUX sont les maîtres. Un physicien est un esclave de son domaine...)

Afin de simuler un système physique par des moyens informatiques, il faut savoir représenter des quantités mesurables afin de pouvoir afficher leurs valeurs. Le problème avec le monde quantique est que les quantités mesurables (les observables) et les résultats de mesure sont des entités de natures différentes ! Aussi l'état du système, qui classiquement est l'ensemble des propriétés observables, est un concept à part... Rappelons les paradigmes fondamentaux de la mécanique quantique :

L'état (pur) est un vecteur (ou "rayon") dans un espace de Hilbert ; on utilise souvent les formes de Dirac : $\ket{\Psi}$, ou $\ket{+1}$, $\ket{u_i}$, etc., comme notation, ce qui est utile quand à l'intérieur du "ket" on peut mettre les paramètres qui le spécifient, par ex. un spin qui a forcément la valeur $+1$ dans le répère de la mesure. On aura besoin du projecteur $P_i = \dyade{u_i}{u_i}$ : opérateur qui réduit un vecteur quelconque $\ket{\psi}$ à un vecteur de sa base : $(\braket{u_i}{\psi})\ket{u_i}$.

L'espace des vecteurs est équipée d'un produit scalaire, complexe, hermitien. $\braket{1}{\Psi}$ en est un exemple, et physiquement $|\braket{1}{\Psi}|^2$ est la probabilité que le système dans l'état $\ket{\Psi}$ donnera la valeur en question quand le spin sera mesuré.
Soyons plus complets : la Nature obéit la règle de Born. Une quantité observable $\hat{A}$ est un opérateur Hermitien (auto-adjoint), décomposable additivement ($\hat{A} = \sum \lambda_i \hat{P}_i$) en projecteurs $\hat{P}_i$ sur ses vecteurs propres $\ket{u_i}$ aux valeurs propres $\lambda_i$, les seules valeurs observables dans l'expérience. La probabilité du résultat est égale à $\opavg{\psi}{\hat{P}_i}{\psi} = \braket{\psi}{u_i}\braket{u_i}{\psi} = |\braket{u_i}{\psi}|^2$.

Le paramétrage d'un système peut être varié. Un système mécanique (particules) peut être décrit par les positions et les vitesses (mais les deux propriétés pour une particule sont complémentaires, le principe de Heisenberg empêche leur détermination conjointe), ou par l'énergie et "phases", etc. Pour les "calculs quantiques" et l'analyse informatique on utilise presque exclusivement les qubits - systèmes à deux états de base, conventionnellement dénotés comme $\ket{0}$ et $\ket{1}$, mais qui peuvent être de nature diverse : un atome avec deux niveaux d'énergie, un spin d'électron (ou d'un nucléon) avec deux orientations fondamentales, un ion dans un piège, etc.

Pour faire des "vrais" calculs, on représente ces états de manière plus concrète que les abstractions de Dirac : $$ \ket{0}=\pmatrix{1\\0}\,,\qquad \ket{1}=\pmatrix{0\\1}\,; \qquad \alpha\ket{0} + \beta \ket{1} = \pmatrix{\alpha \\ \beta} \quad $$ en général, avec $|\alpha|^2 + |\beta|^2 = 1$,... et on a le dilemme qui persiste déjà 80 ans : quelle est l'information "cachée" dans ce système?

Toute mesure, dans tous les systèmes de coordonnées imaginables donnera la réponse "0" ou "1", et il faut disposer d'un nombre infini d'exemplaires du système pour pouvoir évaluer $\alpha$ (sans sa phase ; des expériences plus compliquées pourront mesurer - grâce à l'interférence - une phase relative, mais ceci ne nous intéresse pas). Ainsi un "rotateur" spatial se réduit à un flip-flop. Mais pour les calculs il faut garder la forme générale, et pour un "informaticien quantique" la représentation plus complète, matricielle est indispensable, un bit ne suffit pas.

Cependant, ceci est une "tricherie", le programme dispose d'information qui est "illégale", et qui - vraisemblablement - n'a pas d'existence réelle. Pour un physicien, des abstractions ont des avantages, rendent plus difficile la confusion entre la réalité et son modèle. Pour des informaticiens cette confusion est plus probable (et pour cela chez nous les néoplatoniciens sont plus fréquents que chez vous...)

Je voulais implémenter la physique quantique sans tricher, de manière la plus abstraite possible. On apprend à nos étudiants en cours de géométrie (indispensable pour la relativité, mais aussi pour les quanta, pour la cristallo, pour l'électromagnétisme en général...) que les vecteurs dans un espace avec la structure suffisamment riche sont isomorphes à des applications linéaires (mappings). Ils sont (ou peuvent être) des objets fonctionnels. Et un étudiant de Master saura que l'état d'une particule dans l'espace, décrit par la fonction d'onde de de Broglie : $\Psi(x)$, mais qui peut être représenté dans l'espace des impulsions (Fourier) comme $\Psi(p)$, n'est ni l'une ni l'autre, mais l'abstraction $\ket{\Psi}$, dont les représentants peuvent être $\Psi(x) = \braket{x}{\Psi}\,; \quad \Psi(p) = \braket{p}{\Psi}$. OK, on va manufacturer des applications linéaires...

Construction de l'espace de Hilbert

Supposons que la Nature nous offre un système possédant une propriété bi-valeur, 0 et 1 ou B0 et B1. Nous pouvons définir en Haskell un type de données convenable :

data Qubit = B0 | B1

(ainsi que plusieurs autres, par ex. data Osc = X Double | P Double | N Integer pour un oscillateur ; N est son niveau d'énergie. L'interprétation : B0 : $\uparrow$, B1 : $\downarrow$ est à nous.) Construisons un fragment de programme qui définit ... un espace vectoriel, en profitant de l'universalisme de l'héritage : si le co-domaine des fonctions f admet l'addition, si f x + g x est légal, nous pouvons abstraire : (f+g) x = f x + g x. De telles fonctions sont vecteurs. En Haskell nous pouvons définir des classes de tels types d'objets, qui spécifient les opérations sur ces types :

class Vspace v 
 where
 (<+>) :: v -> v -> v
 (<->) :: v -> v -> v
 (*>) :: Scalar -> v -> v  -- Scalaires : complexes ou réels...

instance Vspace Scalar where  -- Espace trivial pour commencer
 (<+>) = (+)
 (<->) = (-)
 (*>) = (*)
type HV b = b->Scalar   -- Synonyme d'un type fonctionnel

instance Vspace (HV b)
 where
 f <+> g = (\x -> f x <+> g x)
 f <-> g = (\x -> f x <-> g x)
 (a *> f) x = a *> (f x)

Les fonctions sont des vecteurs, mais il faut les "faire". Il est naturel d'accepter une topologie triviale basée sur le fait que deux objets identiques soient identiques, sinon différents ; ensuite on appliquera le théorème de dilatation de Kolmogorov. Définissons un pseudo-produit scalaire, très restreint (0 ou 1).

class Eq a => Hbase a where
  bracket :: a -> a -> Scalar
  bracket j k = kdelta j k  -- Kronecker delta, 0 ou 1.

instance Hbase Qubit
axis :: Hbase a => a -> HV a
axis x = bracket x

On pourra écrire psi = a*>axis B0 <+> b*>axis B1. L'"axe" n'est pas encore un état quantique légitime, sa structure mathématique est trop faible. Mais on voit déjà le "principe d'honnêteté" : axis q, ou psi sont des objets opaques, on ne peut pas trouver facilement leur "contenu", il faut appliquer cette fonction.

"Kets" et dualité.

Les "axes" axis q assimilables à un sous-ensemble restreint de co-vecteurs de "mesure" $\bra{q}$, permettent de définir de manière naturelle les vecteurs d'état $\ket{\alpha}$ : ket alpha. La définition est

ket :: (Hbase a) => a -> HV (HV a)
ket alpha ax = ax alpha   -- ou : ket alpha = \ax -> ax alpha

Cette "application à l'envers" est une construction universelle dans le monde fonctionnel. (C'est le combinateur de Curry ket = flip id). Et de plus, comme un cadeau gratuit, ket a est une fonction linéaire : ket a (ax1 <+> ax2) = (ax1<+>ax2) a = ax1 a + ax2 a = ket a ax1 + ket a ax2. On peut aller plus loin, et mijoter des vecteurs duals aux kets, les "bras" de Dirac, comme des fonctionnelles agissant sur les kets :

(bra alpha) kt = kt (axis alpha)

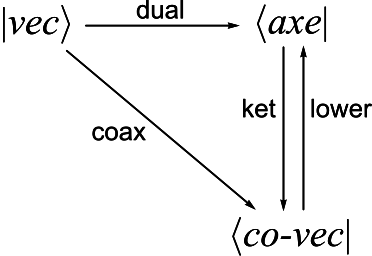triple0 (7K) Ce petit monde est fermé. On peut transmuter un ket vers un axe, grâce à la fonctionnelle dual, ou vers un bra (co-vecteur) grâce à coax. Ou basculer entre un axe (restreint) et un bra général, (mais on ne peut pas faire un ket (vec sur le dessin) :

(dual kt) alpha = conjugate (kt (axis alpha))
(coax kt) kt2 = kt2 (dual kt)
(lower br) alpha = br (ket alpha)

... et on a l'impression que l'on ne fait absolument rien, sauf permuter quelques symboles... Mais quand vous regardez les diagrammes commutatifs dans la théorie des catégories, vous voyez la même pauvreté... On établit un certain nombre de vérités pas forcément évidentes. Dans notre cas tout est implémenté dans un langage de programmation standard, fonctionnel, typé. Exercice. Prouvez que ket unAxe produit un bra. Comprendre le sens du résultat est une autre chose...

Opérateurs

Les opérateurs :

type HM b = HV b -> HV b

appartiennent à un espace vectoriel (évident, non? Le codomaine est une instance de VSpace). Dans la représentation algébrique "classique", les opérateurs sont des matrices, par exemple la négation pour les qubits : $\pmatrix{0&1\\1&0}$ : $\pmatrix{1\\0} \leftrightarrow \pmatrix{0\\1}$. Pour nous ce sont des fonctions, et une classe particulière d'opérateurs sont des dyades $\dyade{\psi}{\phi}$. Un tel objet transforme un ket : $\dyade{\psi}{\phi}\ket{k} = \ldots$, mais on peut imaginer qu'il agisse à gauche, transformant un bra (ou axe) ; ne traitons pas cette question. Soient $\psi, \phi$ des kets. Alors

(kdyad psi phi) kt = kt (dual phi) *> psi

Malgré sa banalité, cette définition nous sera encore utile. La construction des opérateurs adjoints est dans quelques cas universelle et naturelle. Si aop est un opérateur agissant sur les axes, afin de transformer les kets on lui appliquera un "lifting" : kop = boost aop, où :

boost aop unKet = \ax -> unKet (aop ax)

On a l'impression d'empiler des trivialités sur des trivialités. Cependant avec des formules comme ça on peut construire la formule qui donne le spectre perturbationnel complet d'un oscillateur anharmonique...

Un informaticien commence à voir l'intérêt des opérations, quand elles agissent sur des systèmes composites.