Systèmes composites

Pour deux systèmes indépendants on écrit $\ket{\psi}\otimes\ket{\phi}$, $\ket{\psi}\ket{\phi}$, ou même $\ket{\psi\phi}$, mais opérationnellement ceci n'est pas si simple. Il faut calculer le produit tensoriel de deux vecteurs. Avec des matrices, on calcule le produit de Kronecker - ensemble des produits de tous les éléments. Ainsi le ket composite de 10 qubits aura 1024 éléments. Ceci explose vite, le vecteur d'état représentant 1000 qubits ne pourra pas être représenté comme une matrice.

Pour les objets fonctionnels la difficulté est similaire à celle du calcul formel : la prolifération des indices/arguments, $w_{ij} = u_i\cdot v_j$. Un bi-ket primitif, prendra la forme 

ket2 alpha beta = \ax1 ax2 -> (ax1 alpha)*(ax2 beta)
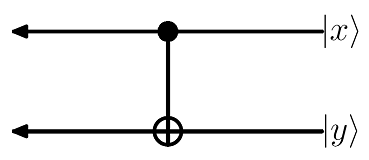cnot (2K) et c'est une fonction de deux arguments, ce qui rend la construction des duals assez délicate. Mais plusieurs opérateurs peuvent être facilement construits, et en particulier la "négation contrôlée", réalisant $\ket{x}\ket{y} \to \ket{x}\ket{x \oplus y}$, où $\oplus$ signifie XOR. De tels opérateurs sont souvent dessinés sous forme de "circuits".


Le bloc CNOT ci-dessus est codé comme 

cnot kt2 ax ay = p B0 + p B1 where
  p b = kt2 (axproj b ax) (xor (axis b) ay)
  axproj alpha ax = ax alpha *> axis alpha
  xor r = r B0 *> id <+> r B1 *> qnot
mais je m'arrête ici, c'est uniquement pour montrer le compacité et la forme du code... Un opérateur 1-qb intéressant est celui de Hadamard, utile quand on veut intriquer deux qubits, de produire une "paire de Bell", avec l'état (par ex.) $\ket{0}\ket{0} \pm \ket{1}\ket{1}$, et autres combinaisons. Toutes ces définitions sont courtes et assez évidentes (et ennuyeuses...). Voici la négation simple, agissant sur un ket : 
qnot = warp B0 B1 <+> warp B1 B0  where
  warp a b kt = kt (axis b) *> ket a

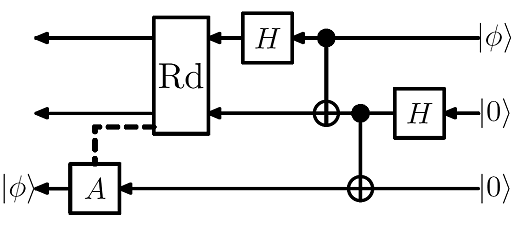tlpcirc (6K) etc. Voici un circuit plus compliqué, qui sert comme modèle de téléportation. Le site émetteur (Alice) intrique le qubit qui doit être téléporté, avec un autre, la moitié d'une paire déjà intriquée, partagée avec le site récepteur (Bob). Alice mesure ses 2 qubits, et transmet classiquement l'information à Bob.


Bob est alors capable - sans connaître son qubit - effectuer une transformation qui restaure celui qui a été massacré par Alice.

Le code a quelques lignes, mais demande le calcul avec des fonctions assez illisbles. A noter : toute manipulation est une chaîne linéaire de transformations, pas de boucles qui utiliseraient une "ligne" qubit deux fois.

Ceci est la consequence que le "jeu" se déroule dans un espace vectoriel, linéaire. Et depuis 80 ans personne ne sait pourquoi la théorie quantique est linéaire... Peut-être c'est une approximation, mais vachement bonne, exacte ! Selon plusieurs "idéologues", derrière il y a une vérité profonde, qui doit être simple.