Python/numpy et traitement d'images

Ceci est une courte digression concernant les transformations géométriques d'images, ce qui est l'essence de l'implémentation des projections cartographiques des rasters : par ex. images satellite. Pour exemple on prendra une projection, jadis populaire, cele de Bonne, mais une introduction plus simple s'impose. En général il s'agit d'une technique de programmation "vectorielle", sans boucles.

Comment faire (peindre) la figure à gauche? Il ne s'agit pas de la dessiner, de tracer et remplir le contour. Nous voulons trouver, et implémenter un objet mathématique qui représente ce disque.
Ceci est un disque distordu, facile à décrire en coordonnées polaires. Un disque circulaire, sans distorsion, peut être décrit par la formule géométrique : l'intérieur est là, où $(\vec{x} - \vec{x}_0)^2 < R^2$, les points suffisamment proches du centre y appartiennent, les autres - non. La distorsion consiste à faire varier le rayon en fonction de l'angle azimutal.

L'implémentation de cette figure considère que l'image est un tableau carée, dont les indices représentent les coordonnées dans l'espace, avec l'origine du répère au centre de l'image.
On parcourt le tableau, pixel par pixel, pour chacun on calcule les coordonnées dans un système ce coordonnées convenable, par ex., on suppose que le tableau est le carré 2-unité, avec l'origine au centre. Si la condition géométrique voulue est satisfaite, on place '1' dans ce pixel, sinon - '0' (ceci est conventionnel, bien sûr).

Voici le programme Python qui fait cette figure.

from pylab import *
nn= ... # Taille du tableau. 200, ou 2000, peu importe.
R=0.75; # Rayon moyen, sans distorsion.

def itox(n):
    return -1.0 + 2*n/(nn-1) # Conversion indice → coordonnée
ar=zeros((nn,nn)) # Initialisation

Pour tout point $(x,y)$ on a les coordonnées polaires, notamment le rayon courant $r=\sqrt{x^2+y^2}$. L'angle azimutal est donnée par $\alpha = \arctan(y/x)$, mais pour la programmation on utilise une fonction à deux arguments, qui distingue entre les quatres quadrants : ++, +-, -+, et -- du répère. Donc, $\alpha = \arctan\! 2(y,x)$. Le reste est une double boucle, facile à coder.

for iy in range(nn):
    y=itox(iy)
    for ix in range(nn):
        x=itox(ix)
        alpha=arctan2(y,x)
        rm = R + 0.1*sin(12*alpha); r2=rm*rm
        if x*x+y*y < r2: ar[iy,ix]=1.0
imshow(ar,cmap='gray') # Visualisation

Ceci est tout, et les variantes possibles sont innombrables. On peut ajouter des couleurs, etc.
Pour nn=200 le temps de calcul est de moins d'une demi-seconde. Pour nn=2000, avec le tableau 10 fois plus grand, le nombre d'éléments est multiplié par 100, et le temps dépasse 35 secondes. Aucune chance de traiter les séquences vidéo en temps réel...

Sans une accélération matérielle gràace au parallélisme, pipelining, etc., ce ralentissement est inéluctable. Cependant le vrai problème ici est la lenteur des boucles Python, du code interprété par la machine virtuelle. D'autres machines virtuelles, par ex la JVM peuvent être plus efficaces, mais moins souples. La solutions suivante "délègue" les itérations à la couche implémentée plus "bas", et compilée en code machine.

On commence par la construction des tableaux, de taille conforme à celle du résultat, mais qui représentent directement les coordonnées $(x,y)$.

ax = linspace(-1,1,nn) # Intervalle
xx,yy = meshgrid(ax,ax)

Cette construction produit des tableaux carrés (rectangulaires en général), avec xx contenant toutes les lignes identiques, variant de -1 à 1, et yy – les colonnes identiques, avec les valeurs dans les lignes croissantes.

Ces matrices sont manipulées comme des objets mathématiques.

phi = arctan2(yy,xx)
ar=1.0*(xx*xx+yy*yy < (R+0.1*sin(12*phi))**2)
imshow(ar,cmap='gray')

Pour nn=200 le temps ne dépasse pas 0.07 secondes, mais pour nn=2000 le gain est encore plus considérable : 0.6 s, plus de 50 fois plus rapide.

Ceci ne suffit pas encore pour nos projections cartographiques, car même si nous avons la posibilité de définir globalement les transformations des coordonnées, l'image n'est pas une fonction mathématique...

La technique présentée ci-dessous fait jutement ça, construit une sorte de tableau-fonctions. Ceci est très rarement enseigné, et pas très bien documenté.

Une projection "exotique" : Bonne

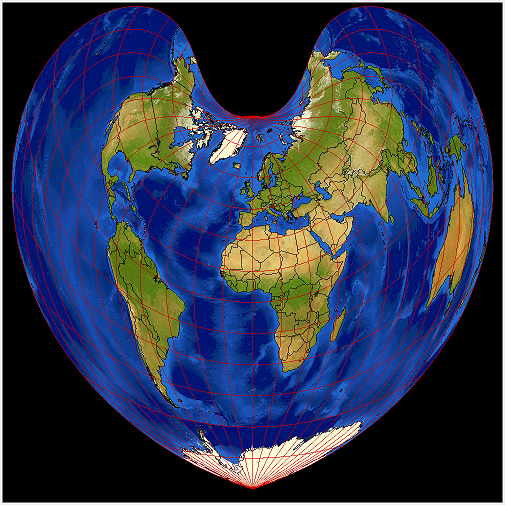Voici la projection nommée après Rigobert Bonne (1727–1795), mais connue avant. Voici la carte de Sylvanus (1511) et Apianus (autour de 1520). La forme est si atypique que l'on a l'impression de voir une création artistique, arbitraire.

Cependant il s'agit d'une vraie projection équivalente, pseudo-conique, où les parallèles sont des cercles concentriques : la même propriété qui concerne les projections polaires, azimutales. Cette projection a été populaire en Europe et en France, utilisée à de buts administratifs et militaires. Seulement durant la première guere mondiale, l'administration a opté officiellement pour le Lambert conique. Actuellement on exploite sa version "dégénérée", la projection sinusoïdale.

Voici les formules, toujours avec le méridien de répère $\lambda_0=0$, le méridien central de l'image.. Il faut choisir aussi un parallèle - répère "standard", noté $\varphi_1$. Si c'est zéro, on obtient la projection sinusoïdale. Pour $\varphi_1=\pi/2$ - la projection de Werner (cordiforme), élaborée également au début du XVI siècle. Alors on définit les paramètres suivants. $$\rho = \cot(\varphi_1) + \varphi_1 - \varphi\,; \quad E = \displaystyle{\frac{\lambda \cos(\varphi)}{\rho}}\, \text{et} \\ x = \rho \sin(E)\,; \quad y = \cot(\varphi_1) - \rho \cos(E)\,.$$ Les transformations inverses, avec $\rho = \pm \sqrt{x^2+(\cot(\varphi_1) - y)^2}$ (le signe est celui de $\varphi_1$) sont : $$\varphi=\cot(\varphi_1)+\varphi_1-\rho\,; \quad \lambda = \rho\displaystyle{\frac{\arctan\! 2(x,\cot(\varphi_1)-y)}{\cos(\varphi)}}\,.$$ On suppose que cette forme particulière est le résultat de la volonté d'améliorer la "projection de Ptolomée", faite autour de l'année 150 (et donc complètement intuitive).

Elle préserve les distances le long du parallèle standard, et les distances verticales. Les parallèles ont la forme de cercles concentriques. Mais ces détails ne nous intéressent pas outre mesure...

Ceci est un exercice en programmation dans le domaine visuel, compacte et efficace. Nous l'avons choisi, car les formules sont assez compliquées, demandant plusieurs observations non-triviales. La construction standard, avec des boucles est la suivante.

from pylab import *
ar=imread("../Images/earth-map-huge.jpg")
ar=ar/256 # Conversion vers flottants normalisés

hh,ww,prf = ar.shape # Dimensions
hh1,ww1 = hh-1,ww-1
lammin = -pi;  lammax = pi
phimin = -pi/2; phimax = pi/2
dlam = lammax-lammin;  dphi = phimax-phimin

# Cible  [carte carrée]
ndimx, ndimy = 400, 400  # ou autres
xlim0 = -pi; xlim1 = pi
ylim0 = -pi; ylim1 = pi
dxlim = xlim1-xlim0;  dylim = ylim1-ylim0

res = zeros((ndimy,ndimx,3))

lambda0 = 0.0
phione = pi/4

sig=1; cot=1/tan(phione)
copa=cot+phione
facl=ww1/dlam;  facp=hh1/dphi
dy = dylim/(ndimy-1); dx = dxlim/(ndimx-1)

for iy in range(ndimy):
    y=ylim0 + iy*dy
    coy=cot-y; coy2=coy*coy
    for ix in range(ndimx):
        x=xlim0 + ix*dx
        rho = sig*sqrt(x*x+coy2)
        phi = copa - rho
        iphi = int((phi-phi0)*facp)
        if (iphi<0) or (iphi>=hh): continue
        lam = lambda0 + rho * arctan2(x,coy)/cos(phi)
        ilam = int((lam-lam0)*facl)            
        if (ilam<0) or (ilam >=ww): continue
        res[ndimy - iy,ix,:] = ar[hh-iphi,ilam,:]
imshow(res); show()

Comme avant, une double boucle, avec des formules sans surprises. Le seul point délicat est qu'une transformation non-linéaire quelconque peut engendrer des coordonnées illégales, en dehors de la carte-source. Il faut donc quelques conditions garde-fous.

La solution sans boucles utilise les mêmes astuces qu'avant.

x=linspace(xlim0,xlim1,ndimx); y=linspace(ylim0,ylim1,ndimy)
xx,yy=meshgrid(x,y)

coy=cot-yy; coy2=coy*coy; rho=sig*sqrt(xx*xx+coy2)

phi=copa - rho
lam=lambda0 + rho*arctan2(xx,coy)/cos(phi)

Ici notre "sagesse" se termine. Nous avons $\varphi$ et $\lambda$ de la conversion inverse depuis xy, mais comment mettre ces données en correspondance avec le tableau ar, sans coder des boucles? Nous pouvons transformer la latitude et la longitude en indices entiers

iphi = ((phi-phimin)*facp).astype(int)
ilam = ((lam-lammin)*facl).astype(int)

mais le reste demande un commentaire un peu difficile.

Indices matriciels

Attention, sujet peu évident, allons doucement. Si on a un tableau, par ex. 2-dimensionnel, disons 3 × 5 : A :

A=array([[100,110,120,130,140],
         [200,210,220,230,240],
         [300,310,320,330,340]])

nous pouvons récupérer ou modifier ses éléments par l'indexation, A[k,j], avec k,j entiers, entre 0 et 2, et entre 0 et 4. Considérons ce tableau comme des "valeurs source", ou "pixels", ces valeurs sont quelconques. Nous voulons construire une "forme - résultat", dont les dimensions peuvent être différentes, par ex. 2 × 3, ou 1- ou 3-dimensionnels, peu importe.
Nous voulons construire le tableau-résultat

res = [[* * *]
       [* * *]]

à partir du tableau A, par le placement de ses éléments dans res. Par exemple, disons que le résultat souhaité est

[[A(2,4) A(0,0) A(0,4)]
 [A(1,1) A(1,3) A(2,0)]]

Grâce à numpy, qui permet l'usage d'autres objets qu'entiers comme indices, la solution est la suivante. On construit deux tableaux contenant les indices ci-dessus :

y=array([[2,0,0],      x=array([[4,0,4],
         [1,1,2]])              [1,3,0]])

Il suffit d'évaluer : p=A[y,x], et on obtient le résultat :

array([[340, 100, 140],
       [210, 230, 300]])

Ceci est l'étape finale de la construction de la projection. Avant, un peu de filtrage, des masques qui éliminent les indices illégaux, en les transformant en, disons, zéros.

iphi = iphi * (iphi>=0)*(iphi<hh)
ilam = ilam * (ilam>=0)*(ilam<ww)*(iphi>0)

res = ar[hh1-iphi,ilam,:] # Direction de l'axe phi
res=res[::-1,:,:] # Direction de l'axe y

Pour l'image 4000 × 4000 le temps de calcul est d'autour de 4 secondes.

Observez que les transformations peuvent être précalculés en toute indépendance de l'image, donc si on veut construire la même projection d'un autre raster, le résultat sortira plus rapidement.

Ceci termine notre digression, mais la maîtrise des techniques vectorielles de programmation, ce qui accélère le développement des programmes, mais ne ralentit pas leur exécution, est en pleine évolution. Tout ceci est adapté au pipelining et l'usage des GPU pour la texturation, indispensable dans le traitement des séquences multimédia, pour les réalisations WebGL, etc.

Actuellement le support de ces techniques sur Android est très limité. QPython pour les tablettes marche, mais plusieurs paquetages sont défaillants ou incomplets. C'est un marché en perspective.