Projections (3)

Projection conique de Lambert

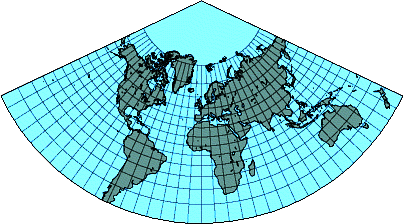Il faut aborder ce sujet, car Lambert conique est la "projection officielle" en France (les détails changent, et le territoire est découpé en zones, donc il ne s'agit pas d'UNE projection. La projection a été adopté par l'artillerie française lors de la 1ère guerre pour des cartes à grande échelle).

La projection est utilisée pour des cartes locales, c'est une famille de projections, parametrée par le parallèle de référence (tangent) $\varphi_0$, ou deux parallèles sécants (fondamentaux, automécoïques) $\varphi_1, \varphi_2$, pour la France : 44° et 49°. (Alors on définit $\varphi_0=0.5\cdot(\varphi_1+\varphi_2)$.) Les formules mathématiques se simplifient avec l'usage du système de coordonées polaires sur le cône, avec le rayon $\rho = \rho(\varphi)$. Nous présentons les simples formules sphériques, mais pour les vraies cartes on utilise les versions ellipsoidales, avec l'excentricité, etc., ce qui est assez compliqué.

D'abord des paramètres auxiliaires :

$$n = \displaystyle{\frac{\log(\cos(\varphi_1)\sec(\varphi_2))} {\log(\tan(\pi/4+\varphi_2/2)\cot(\pi/4+\varphi_1/2))}}\,; \quad F=\displaystyle{\frac{\cos(\varphi_1)\tan^n(\pi/4+\varphi_1/2)}{n}}\,;$$ $$\rho = F\cot^n(\pi/4+\varphi/2)\,$$.

Alors : $x = \rho \sin(n(\lambda-\lambda_0))\,; \quad y = \rho_0 - \rho \cos(n(\lambda-\lambda_0))\,$. (Ici $\rho_0=\rho(\varphi_0)$).

Les transformations inverses :

$$\rho = \mathrm{sgn}(n)\sqrt{x^2+(\rho_0-y)^2}\,; \quad \theta = \arctan\left(\displaystyle{\frac{x}{\rho_0 - y}}\right)\,;$$ $$\phi=2\arctan\left(\left(\displaystyle{ \frac{F}{\rho}}\right)^{1/n}\right) - \displaystyle{\frac{1}{2}}\pi\,; \quad \lambda=\lambda_0 + \displaystyle{\frac{\theta}{n}}\,.$$

Les paramètres $F, \theta$ sont les mêmes que dans les formules directes. Ces formules ne sont pas à mémoriser, et leur dérivation aurait pris trop e temps, mais elles sont utilisables pour implémenter le codage des simples cartes, comme celle d'Europe, montrée ci-dessus.

Projections azimutales variées

Projection stéréographique

La projection azimutale, directement sur un plan par des rayons parallèles ("photographique") préserve rseulement les directions radiales, elle est purement visuelle, intuitive. Mais il existe une projection focale, centrée non pas sur une "caméra", mais sur "l'autre bout" de la sphère. Cette projection est conforme, et puisque les angles sont préservés, les directions depuis le centre de la carte aussi. Nous pouvons donc montrer les propriétés de la transformation sur une section 2D.

Si on mesure l'angle - élévation dans $[-\pi, \pi]$ depuis la verticale, on voit que le rayon $x = 2R \tan(\alpha/2)$. Le "pôle nord" est projeté sur l'infini. Donc, cette projection est incapable de rendre intégralement la surface de la sphère. (On peut, bien sûr, re-projeter le plan sur un disque de rayon fini, mais c'est une autre projection).

Voici deux projections depuis le pôle Sud, avec deux rayons (angles) limites, 70° et 140°.

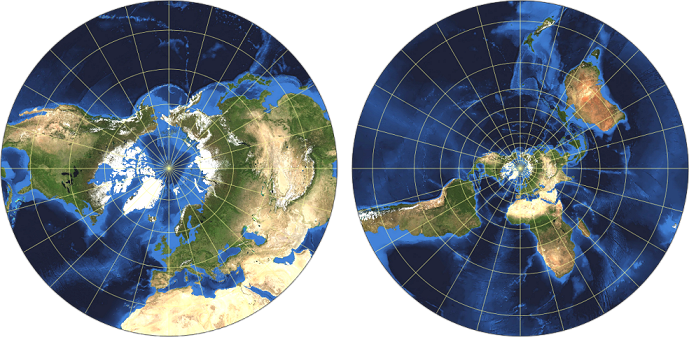
Il est possible de voir les zones polaires depuis l'équateur, si l'angle limite dépasse 90°. Ici : 120°.

Cependant il est évident que si on a besoin des formes qui ne s'éloignent pas trop des originaux, il faut mieux se limiter aux angles limites qui ne dépassent pas 90°.

Cette projection a inspiré d'autres, par ex. celle de Braun, une projection cylindrique stéréographique, les rayons de projection partent des points opposés à ceux de la tangence. (C'est une projection cylindrique classique, avec les rapports des hauteurs différents de la plate carrée, Lambert et les autres...) Le paramétrage, le choix de la normale $\vec{A}(\lambda_0,\varphi_0)$ est essentiel, et les formules sont peu lisibles ; le raisonnement 3D présenté lors de la discussion de la projection ortho est applicable, sauf que la formule $\vec{p} = \vec{x} + C \vec{A}$ n'est plus vraie. Le "pôle" a la position $-\vec{A}$, et $\vec{p} = K \cdot (\vec{x}+\vec{A})$ (soustraction de $-\vec{A}$).

Projection gnomonique

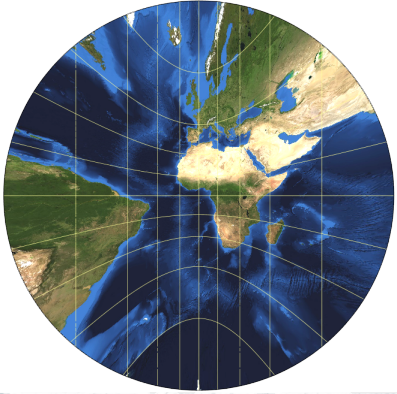Ceci est une projection mathématiquement intéressante, mais qui produit de telles distorsions, que l'on la voit très rarement. Sa construction est similaire à celle de la stéréographique, mais le centre de la projection est le centre de la sphère.

Elle ne peut donc rendre même une hémisphère (entre $\pm 90$ degrés), et si l'angle limite dépasse 60°, les distorsions sont cruelles.

Les formules mathématiques sont encore plus simples (pas de soustraction de $-\vec{A}$) que dans le cas stéréographique.

Une projection "exotique" : Bonne

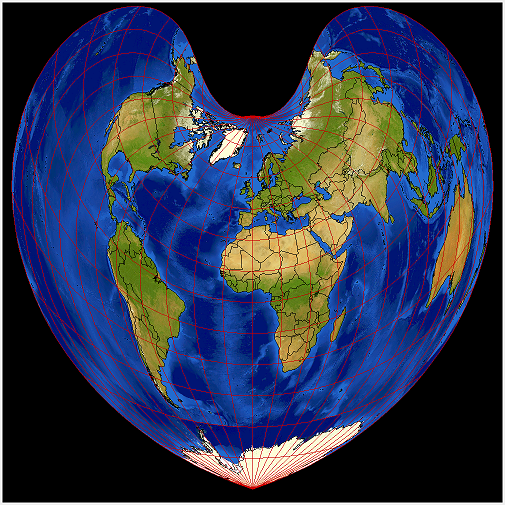Voici la projection nommée après Rigobert Bonne (1727–1795), mais connue avant. Voici la carte de Sylvanus (1511) et Apianus (autour de 1520). La forme est si atypique que l'on a l'impression de voir une création artistique, arbitraire.

Cependant il s'agit d'une vraie projection équivalente, pseudo-conique, où les parallèles sont des cercles concentriques : la même propriété qui concerne les projections polaires, azimutales.

Voici les formules, toujours avec le méridien de répère $\lambda_0=0$.

Mais il faut choisir un parallèle "standard" $\varphi_1$. Alors on définit les paramètres

$$\rho = \cot(\varphi_1) + \varphi_1 - \varphi\,; \quad E = \displaystyle{\frac{\lambda \cos(\varphi)}{\rho}}\,$$ et : $$x = \rho \sin(E)\,; \quad y = \cot(\varphi_1) - \rho \cos(E)\,.$$

Les cas particuliers sont $\varphi_1=0$ qui se réduit à la projection sinusoïdale, et $\varphi_1=\pi/2$, la projection dite de Werner (cordiforme), également au début du XVI siècle.

Les transformations inverses, avec $\rho = \pm \sqrt{x^2+(\cot(\varphi_1) - y)^2}$ (le signe est celui de $\varphi_1$) sont :

$$\varphi=\cot(\varphi_1)+\varphi_1-\rho\,; \quad \lambda = \rho\displaystyle{\frac{\arctan(x/(\cot(\varphi_1)-y))}{\cos(\varphi)}}\,.$$

On suppose que cette forme particulière est le résultat de la volonté d'améliorer la "projection de Ptolomée", faite autour de l'année 150 (et donc complètement intuitive). La projection de Bonne était utilisée en France et ailleurs pour l'usage administratif / militaire, mais au cours de la 1ère Guerre a été remplacée par la projection de Lambert (ailleurs : typiquement par l'UTM).

Elle préserve les distances le long du parallèle standard, et les distances verticales.

Projections discontinues

Ce sont des projections globales qui coupent la surface ailleurs que sur la ligne du changement de date. La mieux connue est la "Goode-homolosine coupée", ci-dessous. Les formules en général sont des combinaisons des plus simples (sinusoïdale, Mollweide), plus des conditionnelles qui ajoutent des décalages horizontaux aux résultats, selon les détails. Ainsi on ne coupe pas les continents.

Nous n'allons pas parler de formules mathématiques, seulement montrer un simple modèle basé sur Sanson-Flamsteed, et ensuite quelques commentaires sur l'approche LSCM "sans math". Comment obtenir cette projection?

Tout d'abord, si on limite les longitudes à des segments, et on ignore les points dehors de ces segments, on obtiendra des cartes partielles, comme ci-dessous à gauche.

Les segments central et droite seront traités de la même façon.

Ensuite, afin d 'obtenir l'image à droite, les points à l'intérieur du segment seront décalés horizontalement, en fonction de $\varphi$. L'équateur n'est pas modifié, le pôle doit prendre la position horizontale qui correspond au méridien central du segment, et entre les deux on interpole.

Pour Goode-homolosine et quelques autres, les coupures ne sont pas complètes. L'utilisateur doir préparer son modèle qui précise les latitudes limites des coupes, et les méridiens de coupure (et les méridiens centraux des segments)

Un découpage presque arbitraire (il faut suivre une "graticule" : les arêtes qui séparent les facettes de la sphère) est possible pratiquement grâce à l'algorithme LSCM (Least Squares Conformal Mapping) integré dans Blender. On modélise la sphère, on spécifie les lignes de coupure et c'est tout. En voici une expérience...