Solutions
Exercice 1.
Voici quelques façons d'importer un document textuel. La lecture d'un texte :
fg = open("../Textes/verne.txt","r",encoding='utf-8')
sg = fg.read()[1:]
(L'élimination du premier caractère ici a eu lieu, car le document avait un marqueur BOM. Ceci n'est pas forcément le cas, attention...)
Si nous ne voulons pas placer le livre entier dans une chaîne, mais lire et traiter ligne par ligne, le fichier peut être considéré comme un itérateur, dont les éléments sont des lignes.
fg = ...
for li in fg:
... li ...
Il ne faut pas oublier que la lecture de cette façon garde le caractère '\n' en fin de ligne dans chaque item.
La lecture d'un fichier à distance, via l'accès http procède comme suit :
from urllib.request import *
fg=urlopen("https://... Textes/verne.txt")
...
Cependant il y a une sérieuse différence entre la lecture d'un fichier, qui est spécifié comme textuel, avec le codage précisé, et l'accès "universel" à un document Web. Partiellement pour des raisons historiques, ce document est considéré comme binaire, et la structure de données obtenue par la lecture (read, etc.) appartient au type bytes, non pas str. Il faut lancer decode, comme signalé ci-dessus, afin de construire une chaîne standard.
Exercice 2.
Voici la construction du dictionnaire des fréquences (normalisées, la somme vaut 1).
fg=open("../Textes/declar_dh.txt","r",encoding='utf-8')
sg = fg.read()[1:]
def freq1(txt):
d={}; n=0
for c in txt:
d[c]=d.get(c,0)+1
n+=1
for c in d: d[c]/=n
return d
d1=freq1(sg)
Vous avez construit ce dictionnaire sans trop de problèmes, sauf ceux qui ont lancé cette procédure sous Python 2, où la division entière tronque le résultat !
Compter les caractères afin de normaliser les probabilités n'est pas nécessaire. Voici une autre stratégie. Lisez-la. Dans les solutions je mentionnerai assez souvent des variantes, dont le but est de vous enseigner quelques techniques de programmation facilitant la vie.
def freq1(txt):
d={}
for c in txt: d[c]=d.get(c,0)+1
cle,val = zip(*list(d.items()))
sumv=sum(val)
for c in d: d[c]/=sumv
return d
La fonction zip "transpose" une séquence de séquences. Si
l1=['a','b','c','d']; l2=[1,2,3,4]; l3=[10,11,12,13]
alors z=list(zip(l1,l2,l3)) donne : [('a', 1, 10), ('b', 2, 11), ('c', 3, 12), ('d', 4, 13)]
(list est nécessaire, car zip seul retourne un itérateur). Cette fonction peut agir comme son propre inverse :
list(zip(*z))
[('a', 'b', 'c', 'd'), (1, 2, 3, 4), (10, 11, 12, 13)]
Exercice 4.
Presque rien à faire.
import nltk
dn=dict(nltk.FreqDist(sg))
Observez la conversion en dictionnaire. Le résultat de FreqDist peut être utilisé comme tel directement, mais c'est une classe spéciale, non pas un dictionnaire...
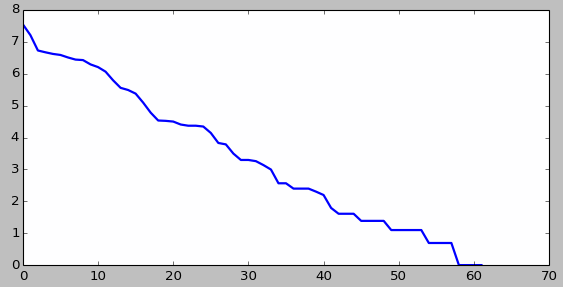Exercice 5.
Le graphique ci-dessous est construit comme en cours : les valeurs (normalisés ou pas) sont triées dans l'ordre décroissant, et affichées comme une courbe dans l'échelle (verticale) logarithmique.
from pylab import *
vals=sorted(d1.values(),reverse=True)
plot(log(vals),'b',lw=2)
show()
Au lieu de calculer le logarithme, on peut demander l'échelle logarithmique dans plot. Lisez la documentation du Matplotlib.
Commentaire pour votre culture générale. Un vieux, très faible système de cryptage consiste à remplacer chaque lettre du texte par un autre symbole. Si le texte codé est suffisamment long, l'analyse des fréquences peut permettre son décodage. Ceci a été exploité dans les nouvelles policières : "Le Scarabée d'Or" d'Edgar Allan Poe (1843), et dans une nouvelle de Conan Doyle : "Les Hommes Dansants" (1898).