Solutions

Exercice 1.

A. Le codage : "aa+b*". L'usage, par exemple :

import re
pat="aa+b*"
r=re.findall(pat,chaîne)

B. Le pattern est "[abc]*b[abc]*"

C. Ceci est un problème récursif, dont la solution avec les regexps est tordue et peu lisible. Nous verrons qu'avec des grammaires non-contextuelles la solution est considérablement plus simple. Aussi, on voit mieux ce qui se passe à l'aide des automates finis.
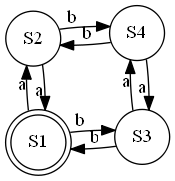
Nous n'envisageons pas parler trop d'automates, ceci est couvert par d'autres cours (même si sera discuté un peu), mais ce problème se visualise à l'aide de l'automate fini à droite. Il est évident que si on commence l'analyse dans l'état S1, "a" nous mène à S2 et "b" à S3. Ensuite soit on revient, ou on trouve l'autre caractère, qui nous dirige vers S4. Alors tout caractère nous rapproche au point initial, qui est terminal. Il doit être évident que cet automate est la réponse.

Dans la pratique courante, l'analyse lexicale qui exploite les regexps utilise les automates. Les regexps sont convertis en automates, dont l'exécution est plus efficace. La transformation inverse a surtout l'utilité pédagogique, le résultat, comme il a été dit, est souvent long et illisible. Plusieurs algorithmes existent, mentionnons un d'eux, simplifié.

Prenons à titre d'exemple l'automate à gauche, à deux états, et analysons son fonctionnement. Intuitivement la solution est claire : pour arriver à l'état terminal S2 depuis Start, il faut une occurrence de "a", suivie par un nombre quelconque de "b". Donc, la solution est "a" | "ab" | "abb" | ... = "ab*".

Ceci est l'intuition. La dérivation formelle a besoin de quelques conventions. Que le marqueur d'état, Start, ou S2, symbolise la chaîne qui nous mènera vers l'état terminal. Si un marqueur satisfait plusieurs "équations", le résultat est leur "somme", l'alternative. Ici : S2=ε (chaîne vide) car il est terminal. Mais aussi
S2 = b S2. La substitution de la première dans la seconde, donne S2=b. Alors, S2=bb en est la solution également. En général : S2 = ε | b S2 possède la solution b*. Et, bien sûr, si S = x | b S, alors S = x | bx | bbx | ... = b*x.

Nous cherchons la solution pour Start, et on voit que Start = a S2, dont la solution est Start = ab*.

Voici un autre exemple. Par définition, S4=ε, et aucune autre chaîne ne pourra être la solution de l'équation pour S4, pas de flèches sortantes. Ensuite, S3 = c S4 = c. Mais aussi : S3 = b S2. Seulement S2 montre une intrication : S2 = b S3. Donc, S3 = c | bb S3, et ceci nous connaissons : S3 = (bb)*c, et Start = a S2 = a(bb)*c.

L'exercice original est plus difficile, car il y a plus d'équations croisées.

S1 = ε ;  S1 = S2 a | S3 b
S2 = S1 a | S4 b
S3 = S1 b | S4 a
S4 = S2 b | S3 a

S1 = ε | S1 (aa | bb) | S4 (ba | ab)
S4 = S1 (ab | ba) | S4 (bb | aa)

S4 = S1 (ab | ba) (bb | aa)*
S1 = ε | S1 (aa | bb) | S1 (ab | ba) (aa | bb)* (ab | ba)
S1 = ((aa | bb) | (ab | ba) (aa | bb)* (ab | ba))*

D. Commençons par un exercice auxiliaire simplifié, qui montre comment coder un pattern qui reconnaît une séquance avec séparateur, qui ne peut avoir ce séparateur ni en début ni à la fin, par ex.: [], [a], [a,a], [a,a,a], etc.
Le pattern en question est : "\[(a(,a)*)*\]" . À présent nous pouvons remplacer "a" par une séquence de chiffres, et ajouter des espaces optionnels. La solution est :
"\[(-?\d+( *, *-?\d+)*)*\]". Récupérer les composantes avec les groupes est difficile, il serait utile de le faire autrement, séparer le contenu entre les crochets, et exploiter split.

Exercice 2.

B. Le pattern est "(?:\+|\-)?\d+(?:\.?[0-9]+)?e?(?:\+|\-)?(?:\d+)?" Attention, vous voyez ici la combinaison " (?: ... ) ", ce qui est spécial (sinon, aucun sens avec la parenthèse ouvrante, qui est méta, devenue optionnelle). Et dans le module re de Python, la forme (?: ...) n'est pas un bloc qui "attrape" le groupe, les parenthèses jouent uniquement le rôle de parenthèses classiques. Ceci élimine la pagaille quand on essaie de récupérer les éléments d'une séquence dont les fragments correspondent au pattern.