Analyse syntaxique. Introduction aux grammaires.

Une grammaire officieusement, est un ensemble de règles permettant de juger si une construction linguistique est "légale". Les grammaires fonctionnent à plusieurs niveaux. Même si les phrases avec des éléments comme le complément indirect, le sujet (év. composite), etc., est largement dominant dans la conscience des gens, on a aussi des règles grammaticales au niveau du lexique, les règles morphologiques, par ex. comment "adverbialiser" les adjectifs (aimable $\to$ aimablement ; furious $\to$ furiously, mocny $\to$ mocno, etc., selon la langue), les règles de conjugaison, de la formation du pluriel, etc.

On peut descendre encore, et analyser les règles de formation des mots au niveau phonétique. Par ex. les mots italiens suivent scrupuleusement des règles euphoniques, tout doit être "facile à prononcer" (pour cela les Italiens sont incapables de terminer un mot par une consonne, rarement, ce sont typiquement des semi-voyelles comme "l", "r", "s", plus des ajouts des consonnes ("a" $\to$ "ed", "a" $\to$ "ad") si le mot suivant commence par la voyelle). La formation des mots composites en Allemand est également codifiée. Mais nous allons nous concentrer sur les structures phrasales plutôt que morphologiques.

La structuration phrasale est importante dans la compréhension des langues naturelles, et de langages formels. On a des constructions syntaxiques comme <sujet> <verbe> <complément>, ou, en programmation : if (x+2*y) > 0 : ..., où les éléments fonctionnent selon le contexte dans lequel ils se trouvent (on a des mots-clés, opérateurs, etc.). Ceci est très important pour la compréhension des requêtes des BD, des dialogues avec un système expert, et dans la compilation.

Les grammaires codifiées existent depuis plus de 2000 ans, et leur évolution progresse avec les sciences en général. Au milieu des années '50 Noam Chomsky a commencé à élaborer une théorie de la syntaxe en vue de la traduction automatisée, et il a formalisé le concept des grammaires génératrices. En deux mots : on dit comment créer des phrases correctes à partir des constituants de base et des règles d'assemblage. Pour Chomski l'important n'était pas seulement "l'ingénierie", mais aussi les aspects cognitifs. On peut poser plusieurs questions : pourquoi les enfants apprennent vite à parler correctement, pourquoi on construit une incroyable richesse de textes à partir d'un nombre fini d'éléments, sans aucune planification globale?...

Est-ce nos structures cérebrales contiennent la notion de grammaire? Il n'y a pas de réponse universellement acceptable à cette question, car elle n'est pas bien posée. Mais Chomsky en général pense que oui, d'autres chercheurs (par ex. M. Halliday : absolument pas).

Pour nous les grammaires seront un dispositif strictement technique.

Commençons par une grammaire (défaillante !) d'un pauvre sous-ensemble du français, mais avec des complications allant assez loin. Elle décrit les phrases genre "ce enragé lion ne réfléchit pas", ou même :
"ce terrible lion qui instruit un terrible chat qui ne mange pas un prof qui chante blesse ce enragé prof qui instruit le mignon chasseur qui ne court pas" selon les règles non-contextuelles de Chomsky.

Montrons la grammaire, et ensuite discutons ses propriétés. Ses éléments sont des constantes littérales, comme "lion", "miaule", etc., et des variables qui décrivent les parties d'une phrase, comme Déterminant, GroupeVerbal, Nom, etc. Quelques méta-symboles déjà vus, comme l'alternative et les parenthèses, seront également utiles. Ci-dessous la concaténantion est simplement l'espace, et "ε" est une chaîne vide. 

Sentence = GroupeNom GroupeVerbal
GroupeNom = DN
DN = Determinant (Adj | ε) Nom ("qui" GroupeVerbal | ε)
Determinant = "le" | "un" | "ce"
Adj = "terrible" | "intelligent" | "mignon" | "pauvre" | "enragé"
Nom = "chat" | "lion" | "chasseur" | "prof"
GroupeVerbal = 
  VNonTran | "ne" VNonTran "pas" | (VTran | "ne" VTran "pas") Compl
VNonTran = "dort" | "chante" | "court" | "réfléchit" | "miaule"
VTran = "mange" | "caresse" | "instruit" | "blesse" | "encourage"
Compl = DN
Les règles syntaxiques sont basées sur les principes suivants :

Une grammaire de ce genre ne dit rien sur le sens des phrases / mots, ou d'équivalence entre des "structures profondes", en dessous de la syntaxe, par ex. "Jean aime Marie" et "Marie est aimée par Jean". Les grammaires capables de traiter les transformations entre les structures profondes ont été analysées par Chomsky, mais le sujet est trop difficile.

On n'échappe pas aux ambiguïtés, au niveau lexical et au niveau structurel, les langues naturelles sont "inexactes". Regardons l'analyse de la phrase "time flies like an arrow".

Le mot "flies" peut être un verbe ou un nom, et d'autres problèmes sont aussi visibles : "fruit flies like a banana" montre une "vraie" structure complètement différente.

L'essentiel est de savoir que si les phrases sont construites selon une grammaire formelle, elles sont analysables. Voici la grammaire ci-dessus en DCG. 

sent --> grNom, grVerbal.
grNom --> detNom.
detNom --> det, (adj | ε), nom, (ε | [qui], grVerbal).
ε --> [].

det --> [le] | [un] | [ce].
adj --> [terrible] | [intelligent] | [mignon] | [pauvre] | [enragé].
nom --> [chat] | [lion] | [chasseur] | [prof].
grVerbal --> vNonTran | [ne], vNonTran, [pas] |
    (vTran | [ne], vTran, [pas]), compl.
    
vNonTran --> [dort] | [chante] | [court] | [réfléchit] | [miaule].
vTran --> [mange] | [caresse] | [instruit] | [blesse] | [encourage].
compl --> detNom.

La requête-test prend une phrase avec des "trous". L'analyse de la conformité avec la grammaire produit le résultat suivant, où la variable Prolog RR dénote le reste de la phrase après l'analyse. 

?- phrase(sent,[le, mignon, prof, qui, X, le, Y, lion, Z, 
   et, le, monde, continue],RR).
X = mange,
Y = terrible,
Z = dort,
RR = [et, le, monde, continue] ;

  % alternative
X = mange,
Y = terrible,
Z = chante,
RR = [et, le, monde, continue] 
...
etc. Le système n'est pas le plus efficace, il y a des algorithmes spécialement adaptés à une telle reconnaissance. Mais les problèmes sont ailleurs. Pour la synthèse un système aveugle est inutilisable, il produira des phrases très longues, empilant récursivement les mêmes terminaux.

Pour l'analyse, l'objectif d'un parseur n'est pas de dire "oui" ou "non" et éventuellement remplir les trous terminaux, mais (par ex.) de présenter l'arbre syntaxique qui en résulte !

On a besoin de gérer : reconnaître, propager, et stocker les attributs (propriétés) des éléments de la phrase analysée.

Ces attributs apportent une information supplémentaire structurelle, permettent de voir et de dire "Succès ! Nous avons reconnu un groupe verbal, le voici : ...", et parfois aussi apportent du sens à la phrase, en filtrant des mauvaises combinaisons (un chasseur ne miaule pas, un prof n'est jamais mignon, etc.)

Les grammaires attribuées sont fondamentales dans l'analyse des langages formels.

Faisons une expérience avec des nombres, et SVP, ne considérez pas ceci comme un exercice avec un langage formel, mais comme avec un langage naturel, celui de l'arithmétique enseignée à l'école. La grammaire ci-dessous reconnaît les nombres entiers : 

dig --> [0]|[1]|[2]|[3]|[4]|[5]|[6]|[7]|[8]|[9].
digs --> dig, (digs | ε).
L'alternative de la seconde clause serait digs --> dig, (ε | digs)., équivalente superficiellement, car la concaténation est associative : $a(bc) \equiv (ab)c$, mais la gestion des attributs serait différente.
Un élève qui effectue l'analyse de la phrase "103281" doit trouver la valeur de ce nombre, son attribut principal.

L'exercice : lire une suite (liste) de chiffres, et en reconstruire le nombre entier qu'elle représente, peut être résolu de plusieurs façons, en voici une, purement itérative : 

nbl = [1,0,9,3,7,4,6,0,8]
def nparse(ch):
    val=0
    for x in ch:
        val=10*val + x
    return val
Mais ici nous voulons exploiter un algorithme récursif, incorporé dans la grammaire ! On effectuera une "traduction" du "texte séquentiel" en nombre selon le paradigme "syntax-driven translation", la traduction pilotée par la syntaxe. Les attributs attachés aux fragments du texte vont se combiner. On pourra ajouter un détail "mis sous la moquette" ci-dessus : la translation des caractères-chiffres en nombres 0 - 9. Ceci est codé ci-dessous : 
nbch="72100926"; nbl=[ord(x)-ord('0') for x in nbch]

La construction des arbres, nombres, traductions, une analyse des contraintes, etc., est combiner le parsing avec l'analyse sémantique. On est encore loin de l'analyse du contexte psychologique et social du texte, c'est un début... Il faudra comprendre un minimum de programmation en Prolog.

La généralisation est d'ajouter des paramètres aux variables syntaxiques. Ils peuvent être connus (numériques, symboliques), ou constituer des variables logiques (symboles en majuscule), considérées inconnues, et qui s'instancient, récupèrent des valeurs connues. C'est ici que l'on construit et combine les attributs.

L'idée récursive s'exprime par l'exemple : 673 = (10*67) + 3. On détache le dernier chiffre, et la séquence sauf lui. Voici un programme mauvais, qui plante ! 

chfr(N) --> [N],{member(N,[0,1,2,3,4,5,6,7,8,9])}.
nmbr(M) --> chfr(M).  % N : chiffre. {...} : Prolog.
nmbr(V) --> nmbr(Y),chfr(M),{V is 10*Y+M}.
   % et la requête :
phrase(nmbr(Val),[2,4,8,0,1,rien],K).
Val = 2,  K = [4, 8, 0, 1, rien] ;
Val = 24,  K = [8, 0, 1, rien] ;
Val = 248,  K = [0, 1, rien] ;
Val = 2480,  K = [1, rien] ;
Val = 24801,  K = [rien] ;  % et ici le programme se bloque...
On voit ici une règle récursive à gauche. La première chose faite par nmbr est d'appeler nmbr, et ceci est dangereux dans tout langage !. Pourtant, des règles comme ça sont importantes dans la linguistique. Voici une variante qui marche. On ne peut pas simplement détacher le premier chiffre, 673 $\to$ (6; 73), afin de combiner les deux, des informations manquent, par ex. quelle est la longueur de la suite. Mais en regardant l'exemple itératif en Python, on constate l'usage d'une variable-tampon, qui accumule des résultats partiels. Faisons le même récursivement : 
def recpars(l,tmp=0):
    if l: return recpars(l[1:],10*tmp+l[0])
    return tmp
Cet algorithme sera intégré dans le parseur. La définition du chiffre ne change pas. 
nmbr(Val) --> nmbr(Val,0).
nmbr(Val,Tmp) --> chfr(M),{Tmp1 is 10*Tmp+M},nmbr(Val,Tmp1).
nmbr(Val,Val) --> [].
Au lieu de calculer les nombres, nous pouvons assembler les éléments analysés dans des structures symboliques, par ex. gv(...) qui représente le groupe verbal, a(terrible) qui contient la valeur du symbole, et aussi sa classification comme adjectif, etc.

Le code ci-dessous correspond exactement à la grammaire déjà vue, seulement j'a ajouté des paramètres, et reformaté les clauses alternatives. La solution peut être un peu différente, selon la forme de grammaire utilisée. 

sent(sn(A,B)) --> grNom(A), grVerbal(B).
grNom(gn(A)) --> detNom(A).
eps([]) --> [].
Après le parsing, on récupérera une structure sn(...,...), dont les 2 composants forment les groupes nominal et verbal. La "valeur []" retournée par l'adjectif qui manque est redondante, uniquement pour faciliter la reconnaissance du typage de la phrase. 

detNom(dn(D,OA,GN)) --> det(D),(adj(OA)|eps(OA)),
                        nom(N),sub(N,GN).
sub(T,qui(T,X)) --> [qui], grVerbal(X).
sub(T,T) --> [].

det(dt(D)) --> [D],{member(D,[le,un,ce])}.
adj(a(A)) --> [A],{member(A,
          [terrible,intelligent,mignon,pauvre,enragé])}.
nom(n(N)) --> [N],{member(N,[chat,lion,chasseur,prof])}.
Le reste est similaire. La clause adj retourne un adjectif littéral, comme le chiffre dans l'exemple numérique. La clause sub soit rend le sujet composite égal à son noyau, le nom, soit incorpore la sous-phrase "qui ... fait quelque chose". 

grVerbal(gvn(A)) --> vNonTran(A).
grVerbal(gvn('NEG',A)) --> [ne], vNonTran(A), [pas].
grVerbal(gvt(A,B)) --> vTran(A),compl(B).
grVerbal(gvt('NEG',A,B)) --> [ne], vTran(A), [pas], compl(B).
vNonTran(vn(X)) --> [X],{member(X,[dort,chante,court,réfléchit,miaule])}.
vTran(vt(X)) --> [X],{member(X,[mange,caresse,instruit,blesse,encourage])}.
compl(co(X)) --> detNom(X).
Voici quelques tests. 
phrase(sent(Res),[un,prof,miaule]).
Res = sn(gn(dn(dt(un), [], n(prof))), gvn(vn(miaule)))

phrase(sent(Res),[ce,pauvre,lion,ne,chante,pas]).
Res = sn(gn(dn(dt(ce), a(pauvre), n(lion))), 
      gvn('NEG', vn(chante))) 

phrase(sent(Res),[le,lion,qui,dort,caresse,un,chasseur]).
Res = sn(gn(dn(dt(le), [], qui(n(lion), gvn(vn(dort))))), 
      gvt(vt(caresse), co(dn(dt(un), [], n(chasseur)))))
La structure est devenue explicite, ce qui facilite les opérations sémantiques. L'avantage d'utiliser DCG ou d'autres constructions programmées manuellement est le contrôle total de ce que l'on fait, mais souvent il est préférable d'utiliser les librairies, par ex. NLTK. Voici son usage. 
grammar1 = nltk.CFG.fromstring("""
  S -> NP VP
  VP -> V NP | V NP PP
  PP -> P NP
  V -> "saw" | "ate" | "walked"
  NP -> "John" | "Mary" | "Bob" | Det N | Det N PP
  Det -> "a" | "an" | "the" | "my"
  N -> "man" | "dog" | "cat" | "telescope" | "park"
  P -> "in" | "on" | "by" | "with"
  """)

sent = "the dog saw a man in the park".split()

rd_parser = nltk.RecursiveDescentParser(grammar1)

for tree in rd_parser.parse(sent): print(tree)
Ceci affiche : 

(S
  (NP (Det the) (N dog))
  (VP
    (V saw)
    (NP (Det a) (N man) (PP (P in) (NP (Det the) (N park))))))
(S
  (NP (Det the) (N dog))
  (VP
    (V saw)
    (NP (Det a) (N man))
    (PP (P in) (NP (Det the) (N park)))))

Observez que le système a trouvé deux solutions, deux arbres du parsing. Quelle est la différence entre les deux?

NLTK contient pas seulement le compilateur de grammaires qui convertit un texte en classes Python qui effectuent l'analyse de manière similaire aux clauses Prolog (descente récursive), mais aussi est capable de visualiser le résultat de manière graphique.

L'arbre syntaxique peut être soumis à la méthode .draw(), qui affiche le résultat en deux dimensions.

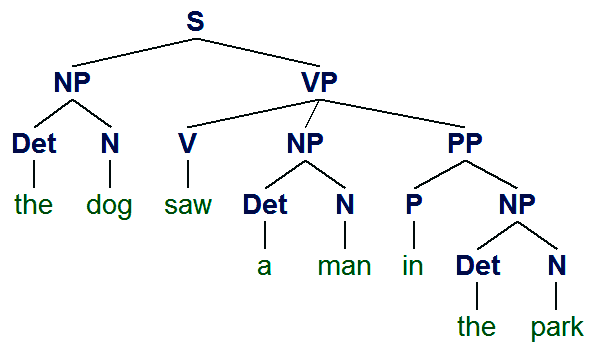Nous arrêtons cette section du cours ici, le reste ce sont quelques exercices. En particulier, nous allons essayer d'engendrer un texte artificiel aléatoire basé sur une grammaire.

La technique n'est pas évidente, car les grammaires non-triviales sont capables de produire des phrases de longueur infinie à cause de la récursivité. Il faudra s'assurer que les variantes récursives soient peu probables.