Implémentation fonctionnelle
paresseuse de quelques
algorithmes co-récursifs

(Un tutoriel, disons,... pédagogique)

Jerzy Karczmarczuk

Résumé. Presque tous les problèmes calculatoires en physique demandent des solutions approchées, ce qui est pénible de plusieurs points de vue, par ex., la gestion des singularités, les dégénérescences, etc. Mais déjà la "surface", le processus d'algorithmisation qui à partir des formules spécifiant le problème - par ex. une équation dynamique engendrée par un Hamiltonien non-linéaire - permet de construire la solution informatique, peut être difficile, et "explosif".

Souvent c'est la conséquence du fait que la représentation / structure "naturelle" du problème soit co-récursive, une "fuite en avant" algorithmique, dont le codage est délicat. Je montrerai sur quelques simples exemples de développement asymptotique (surtout dans le domaine de mécanique quantique), comment le faire à l'aide des techniques de programmation paresseuse (Haskell).

Co-récursion : un court rappel.

Tandis que la récursivité "classique" est réductrice :

fact n | n==0 = 1     -- e finita la commedia
       | otherwise = n*fact(n-1)

la co-récursion, ou apomorphisme, ne demande pas la terminaison (au contraire...), mais chaque pas doit faire progresser l'algorithme.

fact n = rfact!!n where  (!!) indexe la liste : rfact[n]
 rfact = rf 0 1 where
   rf n r = r : rf (n+1) (r*(n+1))

rfact est une "liste infinie", implémentable car ses éléments sont créés au moment de leur usage, quand on demande leur valeur (call by need).

Si une "publicité" de Haskell, affirme qu'un langage paresseux peut opérer avec des listes infinies (comme si quelqu'un en avait besoin)...

Ce n'est pas ça... L'enjeu ici est différent.

Une construction co-récursive est un processus, une dynamique, déguisée en structure de données. Elle est aussi "infinie", qu'un programme qui tourne jusqu'à ce que l'on le casse. (Par ex. un système d'exploitation). La co-récursion est le fondement de l'itération connue sous le nom de mouvement dans l'Univers. Un bébé de 12 mois, quand il commence à marcher, déclenche un mécanisme co-récursif. Il ne faut pas le confondre avec une boucle classique, avec un compteur, ou avec un drapeau booléen testé par son cerveau ; la marche s'arrête car l'enfant, se fatigue, ou tombe...

L'avantage de la formulation co-récursive de la dynamique (solution des équations de mouvement, évolution biologique, et similaires) est l'absence des conditions d'arrêt, de l'"administration" des boucles. Le générateur de la trajectoire, etc. devient plus simple. De plus, il devient plus "physique", au sens de la modélisation structurelle du monde réel.

Exemple. Comment devons-nous engendrer une simple sinusoïde :

Le codage "traditionnel", la liste : $\c y=[\sin(x_0), \sin(x_0+\omega h),$ $\c \sin(x_0+2\omega h), \ldots]\,$, est possible, mais la Nature (une corde de guitare, une flûte, Maria Callas, etc.) ne marche pas comme ça, un oscillateur en hardware n'a pas d'horloge qui mesure le temps (l'argument du sinus), et il s'arrête pour des raisons extérieures.

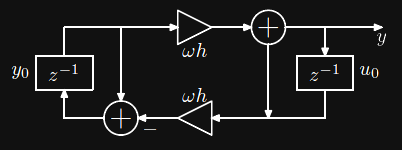Il y a longtemps, j'ai présenté ici des modèles physiques (guides d'onde) d'instruments musicaux, implémentés comme des flots paresseux, co-récursifs. Le plus simple oscilateur monochromatique, est la solution de l'équation : $\c y'' = - \omega^2 y$, ce qui se réduit à deux équations d'ordre 1 : $\color{ora}y' = \omega u$ et $\c u' = -\omega y$. Leur solution par la méthode d'Euler modifiée et stable s'implémente de manière aussi courte : $$ \c u_{n+1}=u_n -\omega h y_{n}\, \quad y_{n+1}=y_n + \omega h u_{n+1} \, $$ mais dont le codage sera (par ex.; autres formes sont possibles)

y = y0 : ((1-(om*h)^2)*>y + om*h*>u) where
  u = u0 : (u - om*h*>y)  -- *> mult. flot par une const.

Ici y est une liste Haskell, une structure de données qui facilite les opérations, comme l'arithmétique, les preuves (co)-inductives de leurs propriétés, la bi-simulation, etc. D'autres modèles de flots existent : Streams, Conduits (similaires aux générateurs Python), etc., et tout ceci progresse, mais restons élémentaires. Les flots peuvent être manipulés itérativement, par ex. ajoutés élément par élément, soumis à des fonction, etc., et ces opérations souvent libèrent le programmeur d'indexer explicitement les éléments, et éliminent les boucles.
Tout ceci simplifie le codage et la présentation des algorithmes.

Un flot $\c u_0, u_1, u_2, \ldots \leftarrow (u_0 :> \bar{u}) $ peut représenter une série infinie formelle : $\c u_0 + u_1 x + u_2 x^2 + \cdots \leftarrow (u_0 + x \bar{u}) $, et de telles séries sont l'essence même de plusieurs calculs de perturbation. Leur manipulation est étonnement simple. ((+) et (-) sont triviaux, "zips".)

(u0 :> uq) * v@(v0 :> vq) = u0*v0 :> u0*>vq + v*uq
(u0 :> uq) / v@(v0 :> vq) = w0 :> wq where
   w0=u0/v0;  wq = (uq - w0*>vq)/v

(v@expr nomme une expr. réutilisée, (:>) a le même sens que (:)).

Appliquer les fonctions élémentaires aux séries est un simple exercice, il suffit de savoir calculer la dérivée et intégrer un polynôme (infini)...

$\c (u_0, u_1, \ldots)' = (u_1, 2 u_2, \ldots) $ ; $\c \int (u_0, u_1, \ldots) = (c, u_0, u_1/2, \ldots) $

exp u@(u0:>_) = w where   -- exp(u)'=exp(u)*u'
     w = integ (exp u0) (w * diff u)

On peut aussi opérer avec des flots - expressions arithmétiques ensemble avec toutes leurs dérivées : [v, v', v'', ...] par rapport à une "variable", qui est également un flot : [v, 1, 0, 0, ...], tandis que les constantes avaient la forme [v, 0, 0, ...]. La différentiation est une trivialité structurelle : df (e0:eq) = eq .

La manipulation de ces expressions est encore plus facile qu'avec les séries :

e@(e0 :- ep) * f@(f0 :- fp) = (e0*f0 :- ep*f + fp*e)
e@(e0 :- ep) / f@(f0 :- fp) = (e0/f0 :- ep/f - e*fp/(f*f))
exp e@(e0:ep) = r where
  r = exp e0 :- (ep*r)

etc. (l'op. (:-) est pour eviter la confusion avec d'autres listes).

Les fonctions élémentaires sont également plus simples.

exp u@(u0:-uq) = w where w = exp u0 :- uq*w
log u@(u0:-uq) = log u0 :- uq/u
sqrt u@(u0:-uq) = w where w = sqrt u0 :- 0.5*>(uq/w)

Ceci permet d'implémenter numériquement une fonction définie par des récurrences différentielles, par ex., Hermite :

$$ \c H_n(x) = \frac{1}{\sqrt{2n}}\left( xH_{n-1}(x) - \frac{dH_{n-1}(x)}{dx} \right)\,, \quad H_0(x) = e^{-x^2/2}\,, $$
ou construire des séries de Taylor "en un clic", par ex. trouvons toutes les dérivées de la fonction de Lambert $\c w(z)$ définie par $\c we^w=z$, utile dans quelques problèmes numériques.
Puisque $ \c {dz}/{dw}=e^w(1+w)$, $\c {dw}/{dz}=e^{-w}/(1+w) $ et on aura :
w = 0 :- exp(-w)/(1+w).

Numériquement : [0, 1, 2, 9, 64, 625, ...].

Le calcul des perturbations

L'occurrence de "petits" paramètres en physique est typique, et les approximations numériques, développement en séries selon ces paramètres [que doivent être des nombres purs, sans dimensions genre masse, longueur, etc.] sont omni-présentes. Ceci ne signifie pas que ces développements soient triviaux, car les les physiciens vivent en permanence dans le voisinage des singularités.

On apprend à l'école que la mécanique classique est la limite de la théorie quantique, quand la constante de Planck $\c\hbar$ tend vers zéro. Mais $\c \hbar=1,054 571 726 \times 10^{-34} m^2 kg / s$ est une quantité dimensionnelle, donc on dit que tout paramètre énergétique d'un système doit être très grand par rapport à $\c\hbar$, ce qui dans votre jardin doit être vrai.
Cependant quand on regarde ce qui se passe avec la fonction d'onde de Schrödinger quand $\c\hbar \to 0$, ...: $$ \c \psi(x,t) \approx \exp\left(\frac{i}{\hbar} S(x,t)\right) $$

On trouve ceci ailleurs (supraconductivité, etc.). Quelques phénomènes de propagation s'expriment par une équation singulière, avec $\c \epsilon $ proche de zéro : $\c \epsilon^2 y'' = Q(x) y $. [Airy : champ E fort, uniforme $\c y'' = Ex y\,; \,\, \epsilon^2=1/E $ ].
L'approximation de Wentzel-Kramers-Brillouin propose : $$ \c y \approx \exp\left( \frac{1}{\epsilon} \sum_{n=0}\epsilon^{2n} S_{2n}(x) + \g\epsilon^{2n+1} S_{2n+1}(x) \c\right)\, $$ où calculer $\c S_{2n}$ est pénible (même si les impairs sont intégrables).

Nous exprimons ceci comme $\c y \approx \exp\left( \frac{1}{\epsilon} S_0 + \g U(x,\epsilon^2) \c + \epsilon V(x,\epsilon^2) \right) $ où $\c S_0 = \pm \int \sqrt{Q}$, ainsi que - en injectant la forme dans l'équation :

$$ \c U' = \frac{-1}{2} \frac{S''_0+\epsilon^2 V''}{S'_0 + \epsilon^2 V'}\,, \quad \c V' = \frac{-1}{2S'_0}\left( U'^2 + U'' + \epsilon^2V'^2 \right)\,. $$
Nous avons des formules intriquées, doublement croisées, qu'aucun physicien traditionnel (Fortranophile) n'osera appeler "algorithme".

$\c U $ etc. sont des séries en $\c \epsilon^2 $, dont chaque terme est une fonction de $\c x $ : non pas une série !, mais qui doit être calculable et différentiable.
N'oublions pas que df est une différentiation sur $\c x $, la queue d'un "flot différentiel".

Pour qu'il agisse sur une série en $\c \epsilon^2 $ on définit dans ce domaine : dfs u = map df u . Alors le codage est la transcription mécanique des formules analytiques ci-dessus :

s0p = sqrt q;  s0b=df s0p
up = (-0.5)*>(s0b :> dfs vp) / (s0p :> vp)
vp = p where 
  p=((-0.5)/s0p) *> (up^2 + dfs up +> p*p)
  (a0:>aq) +> b = a0 :> (aq+b)

(L'opération $ \c a +> b $ signifie $\c a+ \epsilon^2 b$).

Ceci est considérablement plus compact que dans les librairies numériques utilisées par les physiciens.

La condition de progrès fini est assurée, mais ceci n'est pas évident. La génération d'une valeur numérique de, disons, $\c V'(x) $ demande la connaissance de la seconde dérivée de $\c U $, ce qui demande la seconde et la troisième dérivée de $\c V $, et ceci semble être une fuite en avant divergente.

Mais $\c U $ et $\c V $ sont des séries en $\c \epsilon^2 $, et les hautes dérivées apparaissent seulement dans les termes plus hauts.

Il y a des centaines d'exemples de co-récursion extrapolatrice, pas toujours numériques. L'algorithme de remplissage d'un contour graphique par une couleur : si besoin, peindre le pixel courant et ensuite faire la même chose avec tous les voisins, est co-récursif.

Les méthodes présentées ici s'apprennent facilement. Cependant, si on continue à enseigner les calculs scientifiques (et d'autres choses, comme les algorithmes, l'intelligence artificielle, etc.) en présentant surtout des pseudo-codes dans le style des années '60 du siècle dernier, il sera difficile de rendre des techniques fonctionnelles plus populaires...

Perturbations en Méc. quantique

Il s'agit de résoudre l'équation de Schrödinger $\c (H_0 + \lambda V)\ket{\psi} = E \ket{\psi}$, où $\c \lambda$ est un petit paramètre modifiant le Hamiltonien (opérateur d'énergie) ; le point de départ est : $\c H_0\ket{\psi^{(0)}_k} = E^{(0)}_k \ket{\psi^{(0)}_k}$. Ici $\c \ket{\psi}$ dénotent les états quantiques, des vecteurs typiquement infiniment-dimensionnels (ça commence bien...), et $\c E$ sont les énergies que l'on cherche.
Présentons un simple modèle archétypique, dont les variantes sont très importantes : l'oscillateur anharmonique.

On connait la solution non-perturbée, les états d'un oscillateur harmonique. Il est le plus important système quantique de tous, c'est la base de presque tous les systèmes périodiques, et de la théorie des champs en particulier : les niveaux quantiques (d'excitation) sont énumérés : 0, 1, 2, ... N, ... et ces valeurs dénotent les nombres de quanta (photons, phonons, ou autres Schtroumpfs).

Les états appropriés sont notés comme $\c \ket{0}, \ket{1}, \ket{2},\ldots$.

On peut les modéliser comme $\c [0, 0, \ldots, 0, 1, 0, \ldots]$ avec un seul 1 sur la position $\c k$. Notre impléméntation sera finie, mais fonctionnelle. Les énergies non-perturbées sont $\c E_k = \hbar\omega(k+1/2)$. Par la suite, oublions l'énergie du vide $\c 1/2$, et choisissons $\c \hbar\omega=1$. Nous voulons développer les énergies et les états en séries de $\c \lambda$. Voici la technique générale ; plus tard nous définirons $\c V$ comme l'anharmonicité, disons $\c x^4$, seulement il faudra préciser comment $\c x^4$ agit sur $\c\ket{k}$.

On voit la nécessité d'opérer avec des matrices infinies, leur implémentation peut être non-triviale. On cherchera le développement en série :

$$ \c E = E^{(0)} + \lambda\cdot E^{(1)} + \lambda^2 \cdot E^{(2)} + \cdots = E^{(0)} + \lambda \overline{E}(\lambda) $$
et aussi les états perturbés, leurs éléments matriciels $\c \braket{k}{\psi^{(m)}} $.

$$ \c \ket{\psi} = \ket{\psi^{(0)}} + \lambda \ket{\psi^{(1)}} + \lambda^2 \ket{\psi^{(2)}} + \cdots = \ket{\psi^{(0)}} + \lambda \ket{\overline{\psi}(\lambda)} $$

La validité de cette procédure repose sur l'hypothèse adiabatique, que les énergies, etc. sont des fonctions lisses de paramètres et aucune singularité néfaste ne se manifeste ; ceci est faux dans des cas intéressants, où on trouve que les corrections se comportent comme $\c \exp(-\frac{1}{\lambda} F(\ldots))$, par exemple quand l'attraction entre les électrons $\c\lambda\to 0$..., et on voit la transition vers la supraconductivité (condensation de paires de Cooper)... Ici, nous supposons que le schéma marche. On cherchera la correction autour de l'état $\c\ket{0}$ ; $\c E^{(0)}=E_0$, et on pourra noter $\c\avg{k}{V}{m}=V_{km}$. Alors :

$$ \c V\ket{0}+\lambda V\ket{\overline{\psi}} = \overline{E}\ket{0}+(E_0 - H_0)\ket{\overline{\psi}} + \lambda \overline{E}\ket{\overline{\psi}}\,. $$
La cohérence de la normalisation demande $\c\braket{0}{\overline{\psi}}=0$, et les produits scalaires de l'équation ci-dessus avec $\c \bra{0}, \bra{k}$, donnent

$$ \c V_{00} + \lambda \avg{0}{V}{\overline{\psi}} = \overline{E}\,, \\ \c \braket{k}{\overline{\psi}} = \frac{1}{E_0-E_k + \lambda \overline{E}} \big( V_{k0} + \lambda \avg{k}{V}{\overline{\psi}}\big)\,. $$

La première correction énergétique est $\c V_{00}$, ... la troisième peut prendre une journée ou plus, avant même de pouvoir implémenter des formules très compliquées... (la notation n'inclut pas la sommation, des boucles, ni les détails de $\c V_{km}$) ; durant les dernières 90 années ceci a été calculé $\c\infty$ de fois, seulement afin d'obtenir des résultats numériques ; personne n'a besoin de ces formules pour s'inspirer, ou comprendre quelque chose.

Nous devons faire un peu de nettoyage, éliminons $\c \avg{k}{V}{\overline{\psi}} $ qui n'est pas donné directement, et pouvons commencer à coder. On aura besoin de décomposer quelques vecteurs dans la base non-perturbée : $\c \braket{\phi}{\xi} = \sum_k \braket{\phi}{k}\braket{k}{\xi}$. On a :

$$ \c \overline{E} = V_{00} + \lambda \sum_k V_{0k} \braket{k}{\overline{\psi}}\, , \\ \c \braket{k}{\overline{\psi}} = \frac{1}{E_0-E_k + \lambda \overline{E}} \Big( V_{k0} + \lambda \sum_m V_{km}\braket{m}{\overline{\psi}}\Big) $$

Dans ces formules croisées les valeurs inconnues se trouvent "plus loin" dans les séries, et elles deviennent co-récursivement implémentables. Le reste, c'est la programmation en Haskell.

Nous n'avons rien défini pour l'instant, il faut commencer ab ovo, avec la spécification de la mécanique non-perturbée, et ceci demande une certaine connaissance de l'"algèbre des quanta", ce qui ne peut être détaillée ici.

Mais le code est simple. D'abord le code final, ensuite ses éléments :

ebar = v 0 0 :> sum [v 0 k *> psi k | k <- [2,4]]
psi k | k>0 = (v k 0 :> 
        sum [v k m *> psi m | m <- [k-4,k-2 .. k+4]]) / 
            ((-k):>ebar)
      | otherwise = 0

La valeur de ebar est la série : [0.75, -2.625, 20.8125, -241.289, 3580.98, -63982.813 ...].

Le seul élément à décrire est v k m $\, = \c \avg{k}{V}{m}$ ; $\c V=x^4$.

La définition de $\c\ket{k}$ mérite un peu d'effort. On a besoin de la relation d'orthogonalité $\c\braket{k}{m}=\delta_{km}$, et du théorème de dilatation de Kolmogorov, qui élargit une structure algébrique vers un espace vectoriel. Si on définit

cok k m | k>=0 && m>=0 && k==m = 1
        | otherwise = 0

alors l'application partielle cok k représente $\c \bra{k}$, et une autre fonction, qui agit sur les premières : ket n = \f -> f n, est $\c \ket{n}$. Il est facile de prouver que ce sont des vecteurs, comme des fonctions dont le codomaine est numérique : $\c(f+g)x = f x + g x$, mais de plus, les kets sont des fonctions linéaires. On a aussi (ket n)(cok m) $\, = \c\braket{m}{n}$.

Ceci implémente un espace vectoriel $\infty$-dimensionnel, avec la définition naturelle de l'addition (<+>), multiplication par nombres (c#f) : $\c (cf)x=c(f x)$, etc. via applications jusqu'à la réduction aux nombres. Passons aux opérateurs agissant sur les kets, ou les co-kets ("bra"s). Nous aurons besoin surtout de l'algèbre de Weyl, des opérateurs $\c a, a^{+}$ :
$\c \ket{n} \to \ket{n \pm 1}$.

Leurs définitions sont : $\c a\ket{n}=\sqrt{n}\ket{n-1},\,a^{+}\ket{n}=\sqrt{n+1}\ket{n+1} $ ; ils peuvent agir aussi sur les co-vecteurs, ce qui demande deux variantes de codage.
Ces matrices $\infty$-dimensionnelles ont des représentations fonctionnelles très compactes.

ann_C cq n = sqrt n * cq (n-1)
cre_C cq n = sqrt (n+1) * cq (n+1)
ann = boost ann_C
cre = boost cre_C    -- où (par dualité) :
boost f g x = g (f x)

La seule chose qui reste, c'est appliquer le formalisme à la théorie de l'oscillateur, où on apprend que $\c H_0 = a^{+}a$, et que $\c x = \frac{1}{\sqrt{2}}(a+a^{+})$. Chez nous :

v k m = (x . x . x . x) (ket m) (cok k) where
   x = (sqrt 0.5) # (ann <+> cre)

Le code Haskell et la présentation symbolique, sont très similaires.

Il nous faut avouer un petit mensonge, notre calcul de $\c\overline{E}$ est un peu plus compliqué que ça. Le code présenté calcule vite les 8 - 9 premiers termes, et ensuite le programme ralentit ... ensuite nous perdons la patience, ou l'accumulation des thunks, les expressions retardées, déborde la mémoire.

Il faut utiliser la technique de mémoisation, de réutiliser les éléments déjà calculés. Ceci modifie le code :

psi k | k>0 = lpsi !! k   -- indexation, lpsi[k]
      | otherwise = 0 
lpsi = 0 : ps 1 where
   ps k = ((v k 0:>sum[v k m*>psi m|m<-[k-4,k-2..k+4]])/ 
          ((-k) :> ebar)) : ps(k+1)

La gestion de mémoire des programmes paresseux demande parfois de beaucoup de discipline et de connaissance de quelques "astuces du métier".

Mais c'est normal dans tout domaine, sauf si on présente des pseudo-codes, sans jamais avoir mis les mains dans la pâte.

Un exemple de dével. singulier

La "moulinette" co-récursive ne nous libère pas de la connaissance de mathématiques... Prenons une équation distillée des vrais problèmes en physique, une équation récurrentielle avec un petit paramètre $\c \epsilon$, : $\c p = 1 + \epsilon p^5 $. Le codage de la série se réduit à : p = 1 : p^5, et la solution est 1, 1, 5, 35, 285, 2530, 23751, 231880, 2330445, ... Mais un polynôme de degré 5 a 5 racines ; notre solution en donne une seule.

Les quatre autres explosent quand $\c \epsilon \to 0 $, l'équation cache une singularité peu visible à l'oeil nu, sauf si on a déjà eu de l'expérience avec des cas similaires. Alors, l'hypothèse peut être : si la valeur de $\c p $ diverge avec le paramètre allant à zéro, il est possible qu'elle soit proportionnelle à $\c \epsilon^{-\nu}$, avec $\c\nu $ positif. Voici l'argumentation... Définissons $\c p=\g q\c \cdot \epsilon^{-\nu}$.

$$ \c q \epsilon^{-\nu} = 1 + \epsilon^{1-5\nu} q\,; \quad \nu=1/4\, \quad \w \text{fera l'affaire :}\quad \g q = \epsilon^{1/4} + q^5 $$

Développons en $\c\eta$ ($\c = \epsilon^{1/4}$) un $\c q$ tel que : $\c q = \eta + q^5 $. Le terme zéro est un des quatre : $\c q_0 = 1, -1, i, -i$, le cinquième, zéro, c'est cet autre, présenté ci-dessus. Des problèmes de ce genre sont importants, et leurs solutions dans plusieurs articles sont parfois cauchemardesques.

And then, a miracle occurs.... Choisissons q0=1. Afin d'obtenir $\c q(\eta)$, nous allons inverser fonctionnellement $\c \eta(r) = r - r^5$, où r=[1,1] :

r-r^5 = [0,-4,-10,-10,-5,-1,0,...].

Donc, q = srev (r-r^5), où :

srev (_ : v1 : vd) = sscale (1/v1) t where
  vx = (1/v1)*>vd; t = 0 : m;   m = 1 : (-m*m*scomp vx t)
  
sscale c (u0 : uq) = u0 : sscale c (c*>uq) -- u(x)->u(c*x)
scomp u (_ : vq) = sc u where  -- Composition des séries
  sc (u0 : uq) = u0 : vq * sc uq

Le résultat est q = [1.0, -0.25, -0.15625, -0.15625, -0.187988, -0.25, -0.35408, -0.52368, -0.799389, -1.25, ...]. (q0=1 est mis à la main).

Mais on a vu une autre technique : q=integ 1 (1/(1-q^4))...

Il y a plein d'autres exemples. En mécanique classique et astronomie, le cas archétypique, ce sont les corrections non-linéaires d'un mouvement périodique, par ex. $\c y'' + y + \epsilon y^3 = 0$ (l'équation de Duffing avec $\c \omega=1$). On commence avec $\c y = \cos(t)$, et on constate avec horreur que déjà la première correction est :

$$ \c \epsilon\cdot \big( 1/32 (\cos(3t) - \cos(t)) - \g 3/8\, t \sin(t) \c \big) + \ldots $$
avec un terme qui croît linéairement avec le temps. Bien sûr, les techniques appropriées (Lindstedt-Poincaré) existent depuis plus de 100 ans, mais le codage informatique élégant et moderne trouve rarement sa place dans les livres pour les étudiants...

Nous ne pouvons nous arrêter sur ce problème, mais la technique exploite le changement d'échelle de temps, ce qui conceptuellement ressemble à la méthode ci-dessus. Les co-données (év. avec des coefficients symboliques ; rien ici n'est restreint au numérique) est une mine inépuisable d'algorithmes.

Compositions fractionnelles (des séries etc.) : si $\c f^{(3)}(x) \equiv f(f(f(x)))$, alors qu'est-ce que cela représente : $\c f^{(1/\pi)}(x)$ ?
Séries - points fixes des itérations infinies : $\c f(f( \ldots f(x) \ldots ))$, utiles dans la théorie du chaos.
Padéisation, amélioration de convergence, manipulation des fonctionnelles génératrices des graphes, ...
L'implémentation du non-déterminisme logique (backtracking, plusieurs choix de réponses), l'inversion du flot d'un programme, etc.

Etc. Tout ceci est utilisable dans la pratique, et les techniques co-récursives peuvent vraiment économiser beaucoup de temps humain. Donc, je continue à prêcher dans le désert...

Merci

Annexe, Théorie quantique
des champs (en 0 dimensions)

Cet exemple ne montre aucune nouvelle technique, seulement un exemple de l'usage des séries dans un contexte assez cauchemardesque, la théorie d'interaction des particules quantiques. Les particules peuvent se "propager", bouger sans interagir, et aussi émettre / absorber une autre particule.

Quand elle interagissent ad libitum avec d'autres, et aussi avec le vide, qui fluctue et contient des particules virtuelles, on note le "propagateur" et le "vertex d'interaction" comme sur le dessin. Dans la vraie théorie, ce sont des fonctions des impulses, charges, etc. Dans le modèle "0", ce sont des nombres qui dépendent de la "force" d'interaction $\c \gamma$.

Les particules subissent toute interaction imaginable. L'"amplitude d'interaction" 2 → 2 s'exprime par la somme des graphes :

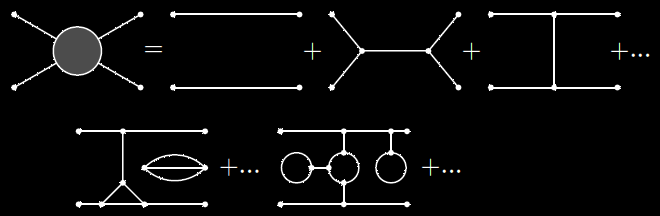où chaque ligne, le propagator libre est une constante que nous pouvons normaliser à 1, et chaque sommet apporte $\c g$. Il y a des facteurs combinatoires à cause de la symétrie quantique, et nous devons évaluer chaque graphe et les additionner.

Ceci est impossible, mais si $\c \gamma$ est petit, on engage la procédure de perturbation, on voudra des séries en $\c \gamma$. Nous devrons aussi tôt ou tard éliminer les "graphes du vide" détachés, qui constituent le fond de la théorie (la notoire énergie du vide), mais ne doivent pas modifier les amplitudes.

Constatons que la structure de ce monde est récurrentielle.

Une bulle d'interaction est un élément primitif qui s'attache à une bulle d'interaction. Ceci est évidemment co-récursif !

Dans une vraie théorie, le propagateur est une fonction $\c G_2(k_1,k_2)$ qui dépend des paramètres de la particule, le sommet est $\c G_3(k_1,k_2,k3)$, etc.
Le propagateur "nu", $\c G^{(0)}_2(k_1,k_2)$ ne dépend pas de $\c \gamma$, d'ailleurs, dépend typiquement d'un seul $\c k$ grâce aux lois de conservation. Le sommet $\c G^{(1)}_3(k_1,k_2,k_3)$ est proportionnel à $\c \gamma$, un "point" : une instance de ce coefficient de couplage.

Une boucle interne, un propagateur cyclique peut contenir des paramètres quelconques, donc l'évaluation du graphe demande l'intégration sur tous ces $\c k$ internes, une procédure très compliquée et singulière. Ceci nous sera épargné...

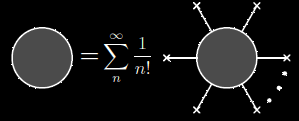Le calcul commence par la construction de la fonctionnelle génératrice des graphes : $$ \c Z[J] = \sum_{n=0}^\infty \frac{1}{n!}G_k(k_1,\ldots,k_n)\cdot J_{k_1}\cdots J_{k_n}\,, $$

ou le graphes à droite, où les $\c J$ sont les variables symboliques, appelées "sources". On peut imaginer qu'une source créé ou consomme une particule, et dans plusieurs théories ce concept est physique, réel.
On somme aussi sur tous les $\c k_i$. En général, c'est une construction permettant d'assembler une collection de fonctions en une entité mathématique. Les "pattes" d'une $\c G_n$ s'expriment par $$ \c G_n(k_1, k_2,\ldots, k_n) = \frac{\partial^n}{\partial J_{k_1} \cdots \partial J_{k_n}} Z[J] \Big |_{J=0}\,. $$

Une dérivation → une patte. Et la totalité de la théorie se réduit à la relation co-récursive à gauche...

Analytiquement, c'est la célèbre équation de Dyson-Schwinger, enseignée à tous les étudiants de la théorie quantique, très vénérée, exploitée pour dessiner des graphes comme ça, et ... et ne jamais ((?), bon...) utilisée pour les calculs numériques. À présent vous savez pourquoi...

Appelons les primitives : $\c G^0_2(k,j) = \Delta_{kj}$, et $\c G^0_3(k,j,m) = \gamma_{kjm}$. Alors : $$ \c \frac{\partial}{\partial J_k} Z[J] = \Delta_{kj} J_j Z[J] + \frac{1}{2}\Delta_{kj}\gamma_{jlm} \frac{\partial^2}{\partial_l \partial_m} Z[J]\,. $$ Comme il a été dit, ceci engendre tous les graphes, y compris déconnectés, dont les poids se multiplient. On se rappelle le théorème fondamental de la théorie des graphes : la génératrice des graphes connexes est le logarithme de la totale. Nous allons travailler avec $\c W = \log Z$, et l'équation D-S :

$$ \c \frac{\partial}{\partial J_k} W[J] = \Delta_{kj}\left\{ J_j + \frac{1}{2}\gamma_{jlm} \left( \frac{\partial^2 W}{\partial J_l \partial J_m} + \frac{\partial W}{\partial J_l} \frac{\partial W}{\partial J_m} \right)\right\} \,. $$
ou, si on veut ...:

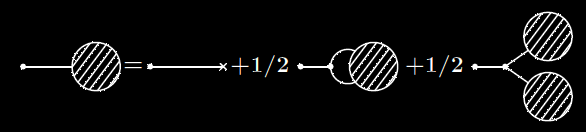
La "fuite en avant" récurrentielle est manifeste. Nous n'avons pas peur, mais simplifions la théorie, en se débarrassant des indices. Un type de sources, pas de paramètres $\c k$. L'équation D-S en zéro dimensions, se réduit à

$$\c \frac{dW}{dJ} = \Delta\left\{J + \frac{1}{2}\gamma\left( \frac{d^2 W}{d J^2} + \left(\frac{dW}{dJ}\right)^2 \right)\right\}\,. $$ L'entité $\c \phi = dW/dJ $ dans la théorie des champs s'appelle ... le "champ". L'équation, avec $\c\Delta=1$, devient $\c \phi = J + 1/2 \gamma \left(\phi' + \phi^2\right)$.

Récapitulons : $\c \phi, W, G_2$, etc. sont des séries en $\c \gamma$, dont les éléments sont des fonctions (expressions différentielles) en $\c J$.

On n'aura pas besoin de $\c J$, c'est zéro,mais pas avant calculer les dérivées. Voici le calcul qui du $\c G_2$ connexe. Il faut prendre $\c W'' = \phi'$, et en sélectionner les têtes (hd), car tout le reste disparaît avec $\c J=0$. C'est tout.

g2 = map hd (map tl phi) where
  phi = (0 :- 1) :> (1%2)*>(dfs phi + phi^2)

ce qui donne : $$\c g_2 = 1 + \gamma^2 + \frac{25}{8}\gamma^4 + 15 \gamma^6 + \frac{12155}{128}\gamma^8 + \frac{11865}{16}\gamma^{10} + \cdots $$
(En 1983, Predrag Cvitanovič a écrit un joli livre sur la théorie des champs, où il montrait le modèle présenté ici, avec beaucoup de calculs. Et il s'est trompé dans le terme $\c\gamma^8$,probablement après plusieurs jours de travail... En 1985, Moritsugu, Inada et al. ont montré comment résoudre l'équation $\c p - \tan p = s$, utile dans l'analyse de la jonction de Josephson, par l'application symbolique de la méthode de Newton-Raphson. Et ils se sont trompés dans le terme $\c (\sqrt[3]{p})^{17}$ ... Mais je ne suggère rien, bien que ...)

L'abominable problème ptan

Nous voulons résoudre l'équation $\c p - \tan(p) = s$, trouver la série $\c p(s)$. Cela commence mal, la série à gauche commence par $\c p^3$, donc la solution sera une série de Puiseux, régulière en $\c x=\sqrt[3]{3s} $. Je rends mes hommages aux nobles samuraïs : Moritsugu, Inada, et Goto, qui ont produit à ce sujet un excellent article de 12 pages, mais il est douteux qu'un vénérable journal accepterait le mien, qui se réduirait à cela :

ptan = -srev (0 :> (-3*>v)^(1/3)) where
   x=0.0:>1; _:>_:>_:>v = x - tan x

dont la valeur : $$\c\small{ -x + \frac{2}{15}x^3 - \frac{3}{175}x^5 + \frac{2}{1575}x^7 + \frac{16}{202125} x^9 - \frac{362}{9384375}x^{11} \\ \c + \frac{49711}{12415528125} x^{13} + \cdots} $$
a quand même un certain avantage. Eux, ils se sont trompés, et moi, je n'avais aucune place où insérer un bug.

Implémentation fonctionnelle paresseuse de quelques algorithmes co-récursifs