Traitement Créatif des Images (2)

Déformation des objets graphiques (raster)

Ceci est un domaine vaste, compliqué, et qui n'est couvert entièrement par aucun logiciel universel populaire, car les objectifs des transformations géométriques des images sont innombrables, les variantes sont infinies, et la plupart de problèmes réels demande une bonne connaissance des manipulations mathématiques sous-jacentes.

• En "standard" les logiciels permettent facilement de changer l'échelle, effectuer la rotation, souvent le cisaillement, parfois la distorsion mais pas plus que ça.
• Quelques programmes de graphisme technique (dont mon préféré, Corel Designer, ex-Micrografx ; Corel a également acheté PaintShop de JASC, et une dizaine d'autres applications souvent initialement gratuites...) disposent d'outils plus universels, on superpose sur le dessin une grille - "envelope" et on la déforme. Le système recalcule les coordonnées des points internes par rapport aux noeuds de la grille, et l'objet est déformé.
  Le Designer est capable de traiter uniquement les dessins vectoriels (on reconstruit la forme depuis les coordonnées des points), avec les images raster, cela ne marche pas.
  
  Cependant une autre application de Corel Graphics Suite, le PhotoPaint, possède un dispositif de warping (envelope) adapté aux images. Si on veut un logiciel gratuit, le WinMorph est très correct, mais vieux.
  
  [GIMP dispose d'un outil similaire, la "cage", mais c'est un plugin fait par un incompétent total, la honte... Je peux faire vraiment mieux. Mais cela attendra ma retraite...]

Images panoramiques.

Sur les déformations (théorie, algorithmique...) je pourrais parler un mois. Si vous voulez une expérience concrète, demandez.

Dans cette section nous aborderons une distorsion très concrète : les panoramas [cylindriques – pour des raisons de simplicité mathématique, mais le problème général est 3D].

Le problème se décompose en plusieurs étapes distinctes

Il faut savoir que les environnements immersifs c'est toute une énorme technologie, avec des centaines d'applications utilisées par plusieurs milliers de personnes. On peut ici seulement gratter le sujet.

La première étape est la construction de l'image (ou d'une collection cohérente, adaptée à UN environnement immersif) qui représente le panorama. Une version cylindrique est ci-dessus. Normalement on la construit depuis des photos normales ("stitching"), et ce processus est compliqué ; des méthodes automatiques marchent mal.

La seconde étape est la visualisation redressée de cette image, la reconstruction d'une projection focale standard depuis le cylindre. La page précédente montre l'applet de Helmut Dersch, qui a été la base de plusieurs autres programmes.

Ceci fonctionne comme si on mettait la caméra au centre de ce cylindre. La projection focale standard, affine, "redresse" l'image, les droites réelles, qui sont devenues courbes, sont restaurées.

Ceci fonctionne également en 3D complet, 4π stéradians. Pour faire des tests on n'a pas besoin d'une applet spéciale. Lors de mon cours d'magerie, j'utilisais soit VRML, soit un logiciel de rendu 3D interactif (Blender). J'assemblais "physiquement" le cylindre, texturé avec l'image panoramique, et sans aucune formule ni programmation [autre que la modélisation], j'avais l'effet.

En passant... Pour le 3D immersif complet, on peut utiliser soit un mapping sphérique, l'équivalent d'une non-projection cartographique connue sous le nom de carte équi-rectangulaire (mais cette mappe-monde est vue de l'intérieur...), soit l'environnement cubique : l'observateur est plongé dans un cube dont les 6 facettes constituent son environnement visuel. Pour 2D : 4 facettes.

Cependant les images doivent être obligatoirement grand-angle, 90° minimum (courte focale), sinon on ne collera pas les 4 images, il en faudra plus.

Commençons par l'analyse d'une seule image standard. Il faut "coller" une image plate sur un cylindre. Ou, au contraire, re-plier le cylindre, mais non pas comme si on le faisait à la main, mais avec la projection focale (gnomonique).

Une propriété importante qui va nous aider est, que les dimensions absolues n'ont pas d'importance. On peut choisir le cylindre de rayon quelconque, et placer l'image (ou une scène réelle 3D équivalente) à la distance quelconque de la caméra.

Les formules mathématiques sont triviales, niveau BAC (ce qui implique que mes étudiants niveau Master M1 ou M2 avaient des sacrés problèmes avec...)

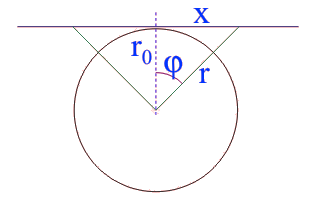
On voit clairement que l'angle \(\varphi\) est la distance sur l'image panoramique. Pour cet angle, \(x\) vaut \(r_0 \tan(\varphi)\), ou \(r_0\) est le rayon (figé, mais conventionnel, on peut le fixer à 1) du cylindre. La distance entre la caméra et le "point redressé" est égale à \(r = r_0 / \cos(\varphi)\).

Le rapport \(r/r_0\) est le taux d'augmentation de la dimension verticale de cette tranche \(x, \varphi\). Et c'est tout, le reste est l'ajustement des coordonnées aux dimensions de l'image en pixels. Un simple visualiseur cylindrique fait en TP, est un programme javascript d'une douzaine de lignes, dont la plupart est "administrative".

Anaglyphes

Filtres, filtres...

  →