Représentation fonctionnelle
des objets quantiques

(Domaine : Informatique, mais aussi un peu de philosophie des sciences...)

Jerzy Karczmarczuk, 2018

Attention, nous montrerons un peu de programmation en Haskell

Entre calculs et modèles

Pour les entités élementaires, les qubits (hélas, 90% d'informaticiens n'ont aucune notion concernant d'autres systèmes...), on écrit des formules de superposition : $\ket{\psi} = \alpha\ket{0}+\beta\ket{1}$, où $$\ket{0} = \ve{1}{0}; \quad \ket{1} = \ve{0}{1} \quad \to \ket{\psi} = \ve{\alpha}{\beta} $$ etc.

Mais on sait que $\alpha$, $\beta$, ... n'ont aucun sens observationnel, on ne peut les mesurer pour un système individuel (et c'est pire que la pression d'une seule molécule de gaz).

Depuis 100 ans on n'a la moindre idée quelle est l'ontologie d'un système physique, qu'est-ce qu'il "est"? (quelles sont ses propriétés intrinsèques mesurables, indépendantes. Entre l'ontologie et l'épistémologie il y a un abîme infranchissable, car

Toute (ou presque) observation modifie le système...
La MQ ne dit rien d'observationnel sur un individu (qubit etc.), un état quantique établit seulement la distribution statistique d'un ensemble de systèmes.
En fait, on ne sait pas quel est le sens de ce que l'on appelle "l'état quantique". Même le nom "état" a été choisi arbitrairement.

On dit que l'état (ses paramètres) évolue dans le temps, selon l'équation de Schrödinger, et les quantités "observables" sont des opérateurs/matrices indépendants du temps. Mais c'est faux, ou plutôt : conventionnel. Dans la représentation de Heisenberg (Heisenberg picture) ce sont les observables qui évoluent, l'état reste figé depuis le début de l'Univers... Qu'est-ce que l'on modélise?

Sur le plan calculatoire ceci ne pose pas de problèmes. La valeur moyenne observable d'un opérateur $A$, change avec l'opérateur unitaire d'évolution $U$ (typiquement $U=\exp(-iHt)$) : $$ \avg{\psi}{A}{\psi} \quad\to\quad \avg{\psi}{U^\dagger AU}{\psi}$$ mais sur quoi agit $U$?... On choisit. (Dans la théorie quantique des champs on utilise une variante dit d'interaction, où les deux entités changent, mais de manière différente.

Les calculs en physique progressent : on a un modèle, et on calcule les trajectoires, les distributions statistiques, les énergies... On résoud les équations différentielles, calcule les valeurs propres des matrices, lance l'intégration Monte-Carlo, etc. Mais si on veut plus, si on veut vraiment modéliser (ou simuler) un système?... Il faut implémenter des objets mathématiques abstraits, mais respectant des tas de subsomptions. Et l'ordinateur n'a pas la patience de papier.

Quelques exemples

Quel genre de calculs l'ordinateur peut faire sans trop de travail préparatoire humain? Il est adapté aux manipulations algébriques, discrètes, et au numérique "standard". Et aussi à la génération des objets graphiques, mais ici cela ne sera pas important.

Dans le domaine d'"info quantique" (whatever this means...) on aime bien – à des buts pédagogiques – présenter des algorithmes à l'aide des "circuits". (Ma convention est contraire à tous les autres, et elle est cohérente vis-à-vis l'écriture : le temps va de droite vers la gauche; dans l'expression $\hat{O}_1 \hat{O}_2 \cdots \hat{O}_n \ket{\psi}$, l'opérateur $\hat{O}_1$ agit en dernier). Les boîtiers sont des opérateurs, d'utres éléments seront décrits plus tard.

La figure dessus représente le circuit de Deutsch. Étant donnée une fonction inconnue $f$ d'un seul bit, il faut répondre à la question si c'est une fonction constante, disons, zéro pour tous les arguments, ou "équilibrée": $f(x) = x$. L'idée est de faire cela d'un seul coup, grâce à la superposition. C'est un jouet, mais instructif.

Ceci est un circuit de téléportation : le transfert d'un qubit inconnu vers une destination lointaine. On n'a pas le droit de le mesurer !
(Mesurer un état quantique l'anéantit, il "devient" un des vecteurs de base en vigueur, et il n'a plus rien à voir avec Captain Kirk).

C'est le téleporteur qui effectue la "mesure", et détruit l'original, puisque le clonage est interdit par la Force Supérieure (l'unitarité).

Plusieurs autres circuits sont intéressants, par ex. la recherche d'un pattern, à l'aide de la transformée de Fourier quantique, mais c'est trop compliqué pour l'aborder ici.

Finalement, notre calcul d'un autre genre, c'est de la physique, non pas le jeu formel avec les qubits. La base standard (de Fock) d'un oscillateur harmonique, est une famille d'états $\ket{n}$, avec $n=0, 1, 2,\ldots$ représentant le niveau énergétique.

Le Hamiltonien (ne pas confondre la lettre $H$ avec l'op. Hadamard, ci-dessus !) de l'oscillateur libre est $H = p^2/2 + x^2/2$, ce qui peut être formulé par les opérateurs de création $a^+$ et d'annihilation $a$, comme $H = a^+ a + 1/2$. (Tout sera expliqué plus tard).

Nous voulons calculer les corrections aux énergies pour l'oscillateur anharmonique, avec le potentiel $V(x) = x^2/2 + \lambda x^4$.

La correction (1) est normalement décrite en cours de Mécanique quantique, son calcul prend moins de 10 min. La correction (2) est une petite galère, comptez quelques dizaines de minutes, et quelques feuilles de papier, avant d'obtenir un nombre.
La correction (3): au moins une - deux journées, c'est une punition très cruelle pour les étudiants. Ensuite la complexité explose.
Je montrerai comment obtenir toutes les corrections, d'ordre quelconque (la mémoire de l'ordinateur et le temps ne permettent pas aller trop loin).

Il n'y aura aucune équation différentielle à résoudre, toute numérique est élémentaire, par contre nous aurons besoin de la "paresse" du langage Haskell, afin de travailler sans soucis avec une liste infinie.

Pour cet exercice on n'a pas besoin de mon modèle conceptuel, c'est orthogonal par rapport à la continuation de mon exposé, mais la philosophie d'utiliser un langage fonctionnel dans ce domaine, reste la même.

Je voulais concevoir et implémenter concrètement, dans un programme, un modèle de mécanique quantique sans "tricherie", dans la mesure du possible. Eviter d'opérer sans vergogne sur les quantités, que nous ne sommes pas censés de connaître.

La philosophie est minimaliste, on ne réinvente pas la mécanique quantique, il s'agit simplement de formuler une technique de programmation assez abstraite, beaucoup plus abstraite que les approches normalement enseignées.

L'interprétation de Copenhagen ne change pas, la projection d'un état $\ket{\psi}$ sur un vecteur de base $\ket{k}$ dans l'espace de Hilbert du système, l'amplitude $\psi_k = \braket{k}{\psi}$, spécifie la probabilité $p_k = |\psi_k|^2$ de trouver le système dans cet état. Dans mon exposé on va quand même "inventer" quelque chose : l'espace de Hilbert ex machina...

Nous allons utiliser la programmation fonctionnelle pure et le langage Haskell. Ceci demande une introduction.

Le programme est composé de définitions de fonctions, et une expression. Pas d'instructions (ou de commandes). On peut affecter une variable : x=17/(1-y), qui devient synonymique avec sa valeur, mais on ne peut plus la changer ! Dans les quanta on passe d'un état à l'autre, mais pas de "propriété" d'un objet qui "change".

Les fonctions en Haskell sont opaques et "abstraites", on ne peut les analyser, seulement passer à autres fonctions ou les appliquer. Analogie : Dans le monde quantique on ne peut analyser et reconstruire (cloner) un état, il est opaque et abstrait, et son clonage violerait l'unitarité (la cohérence de son système probabiliste).

Il est facile, grâce au "protocole normal" d'évaluation, "cacher" l'information dans les fonctions. Exemple, définissons une fonction partielle d'addition:

add x y = x+y
ad3 = add 3    -- arg. omis -> "fonction de"... ad3 2 -> 5

On ne peut extraire l'information sans "détruire" la fonction en l'appliquant. Ceci modélise ce "secret quantique", et permet que le langage définisse des structures de données, sans structures de données. Voici "paire(x,y)" comme une fonction:

(pair x y) c = c x y  -- et comment extraire x,y?
first a b = a    -- ou : first = const, prédéfini
second a b = b   -- ou : second a = id, prédéfini
struct = pair 42 (-7)   -- création d'un objet opaque

On peut obtenir quelques résultats par : struct first, ou struct add, mais l'opacité n'est pas violée.

"Création de l'univers quantique" (ou : "quantisation fonctionnelle")

L'assignation numérique des spécifications des états quantiques est conventionnelle, "abstraite". Dans $\ve{1}{0}$, le "1" n'a rien à voir avec un, ou "0" avec 0. On pourrait écrire $\ve{+}{-}$ ou $\ve{↑}{↓}$. Les états d'un oscillateur $\ket{n}$: $\ket{0}$, $\ket{1}$, $\ket{2}$ dans la représentation de Fock sont numérotés ex post; on sait, que les énergies associés à ces états (niveaux), constituent une suite arithmétique (nombres de quanta ["photons"?] dans le champ).

Commençons la création de l'Univers, par la paramétrisation des entités observables. Pour un qubit, c'est une paire, par ex. 'B0' et 'B1', ou autre chose. Un oscillateur peut être vu comme un point qui bouge (position spatiale), ou comme un champ (niveau entier ≥ 0). Ce seront nos données de base (ou le substrat, que nous appelerons QBase).

data Qubit = B0 | B1
data Oscil = X Double | P Double | N Integer | Z Complex
-- (Z c'est la paramétrisation par les états cohérents...)
-- ...
data IsoPion = Posit | Negat | Neutr
-- etc.

Cette paramétrisation ne contient aucune propriété mathématique, sauf la reconnaissance des valeurs, ce qui implique l'existence de l'égalité. Mais, avec un minimum de postulats, un raisonnement naturel, universel, catégoriel, permet de déduire beaucoup de choses concernant la structure formelle de nos entités. et ceci constitue le point le plus important de cet exposé :

Si le substrat $\Gamma$ contient a, b, c,... quelconques, mais on postule l'existence des fonctions avec le co-domaine numérique (disons, une sorte de "mesure", très restreinte, f :: $\Gamma \to$ Nombres), nous avons un espace vectoriel fonctionnel, car (f + g) x = f x + g x; ($\alpha$*f) x = $\alpha$*f x.

De plus, si on construit l'espace dual, des fonctions sur ces fonctions (cela commence à être un peu ennuyeux, mais on fait des choses comme ça en permanence, par ex. en géométrie), – il est facile de montrer que nous aurons une théorie linéaire, pas seulement un espace vectoriel, mais l'espace d'applications linéaires, ce dont on a besoin pour les quanta : le produit scalaire est (sesqui)linéaire, les observables sont des opérateurs linéaires, l'équation de Schrödinger est linéaire, c'est l'essence du principe de superposition !

(... et depuis 80 ans on ne sait pas pourquoi ... )

Quelles fonctions?...

Définissons une fonction d'identification / distinction. Appelons-la bracket, mais le nom - synonyme axis sera utilisé plus souvent.

bracket a b = if a==b then 1 else 0

Soit on est une chose (oui), soit l'autre (non) (sur le plan classique, superficiel). Nous avons ainsi nos fonctions - vecteurs

axis a = bracket a            -- ou, si on préfère :
axis a = \b -> bracket a b    -- lambda: fonction anonyme

Ces "axes de mesure" sont trop restreints, pour constituer l'espace des états. Il nous faut un espace plus élaboré, mais construit de manière universelle, indépendante du système. Ce sera une opération de dualité, une "application inverse"

Construisons une fonction appelé (après Dirac) ket , et parametré par les données du substrat: B0, B1, ou le niveau de 'oscillateur, ou la position de la particule, etc. Cette fonction agira sur les axes, et retournera un nombre. L'essentiel est, répétons encore une fois: que la construction soit universelle. Pas d'inventions ad hoc.

Kets et dualité

Que l'argument ax dénote un axe, et $\alpha$ – une donnée du substrat. Définissons

ket alpha ax = ax alpha  -- fonction agissant sur une autre...

Ce formalisme, qui semble assez vide, nous apporte un cadeau inattendu, (ket alpha) est une fonction linéaire ! Étant donnés deux axes, ax1, ax2 :

ket alpha (ax1 + ax2) = (ax1 + ax2) alpha
  = ax1 alpha + ax2 alpha
  = ket alpha ax1 + ket alpha ax2

Désormais nous pouvons identifier ket alpha avec un vecteur de base $\ket{\alpha}$, et
ket alpha ax est $\braket{\mathrm{ax}}{\alpha}$.

Cela ne suffit pas pour disposer d'un espace métrique, le "bracket de Dirac" avec ses priopriétés habituels, nécessite l'espace bidual par rapport aux axes, $\bra{\alpha}$ sera une fonction agissant sur les kets, une application forcément linéaire, qui n'est rien d'autre, que notre rêvé produit scalaire. Le monde est clos.

(bra alpha) kt = kt (axis alpha)

Le système est cohérent, vérifions $\braket{\alpha}{\beta}$:

bra alpha (ket beta) = ket beta (axis alpha)
   = axis alpha beta ≡ bracket alpha beta

Toute cette manipulation sur le plan mathématique est presque totalement triviale, mais nous avons travaillé dans l'« esprit informatique ».

Nous avons forcé l'ordinateur à implémenter le théorème de dilatation de Kolmogorov.

Si l'application $K: X \times X \to \mathbb{C}$ est définie positive, $\sum_{i,j}K(x_i,x_j)\xi_i\bar{\xi}_j \ge 0$,avec $x \in X$, et quelconques $\xi \in \mathbb{C}$, alors il existe un espace de Hilbert $H_K$, et une application $v_k : X \to H_K$, telle que $\braket{v_K(x)}{v_K(y)} = K(x,y)$.

La bi-linéarité du produit scalaire est assurée. Les propriétés complexes demandent un peu de travail (trivial), pour s'assurer que $\braket{b}{a} = \overline{\braket{a}{b}}$.

Nous pourrons alors construire les opérateurs, et convaincre l'auditoire que tous les calculs en informatique quantique sont réalisables dans le cadre de ce formalisme.

Construisons les fonctionnelles ci-dessous. La fonction dual transforme un ket en axe, coax : un ket en bra, et lower : un bra en axe. (D'ailleurs coax n'est rien d'autre que le produit scalaire, le "bra-ket" de Dirac.)

(dual kt) alpha = conjugate (kt (axis alpha))
(coax kt) kt2 = kt2 (dual kt)
(lower br) alpha = br (ket alpha)

Il n'existe aucune méthode universelle de construire un ket (la conversion d'un axe inconnu).

On a l'impression que l'on n'a rien fait, sauf permuter quelques symboles... Mais quand on regarde les diagrammes commutatifs dans la théorie élémentaire des catégories, on voit souvent la même pauvreté structurelle.

Ayant deux kets : $\ket{\phi}$ et $\ket{\psi}$, la forme $\braket{\phi}{\psi}$ : scalprod phi psi est

psi (dual phi)  -- Prouver: = conjugate (scalprod psi phi)

Notation

Un peu de Haskell... L'ordinateur ne sait pas comment "ajouter deux fonctions", les propriétés mathématiques doivent être explicitées. Nous définissons les classes correspondantes. (Rien de nouveau, il suffit d'y jeter un coup d'oeil...)

type Scalar = Complex Double  -- ou autre chose
class Eq a => Qbase a where   -- égalité : prémisse nécessaire
 bracket :: a -> a -> Scalar
 bracket j k = kdelta j k
axis alpha = bracket alpha    -- synonyme

instance Qbase Qubit
instance Qbase Oscil where
  bracket (N j) (N k)
   | j>=0 && k >=0 = kdelta j k -- pas de niveaux négatifs
   | otherwise = 0

class Vector v where       -- v est un el. d'espace vectoriel
 (*>)   :: Scalar -> v -> v
 (<+>)  :: v -> v -> v
 (<->)  :: v -> v -> v

Pour simplifier et désambiguër la notation :

type QV b = b -> Scalar      -- axes
type QK b = QV (QV b)        -- kets
...
instance Vector Scalar where
 x  *> y  = x * y 
 x <+> y  = x + y  -- etc.
instance (Vector b) => Vector (a -> b) where
 (a *> f) x = a *> f x
 (f <+> g) x = f x <+> g x   -- etc.

Ici b est un Vecteur quelconque, QV b, QK b etc. est OK, récursivement.

Ici on met les définitions de nos f. primitives : ket, dual, bra, etc.

...
scalprod v w = w (dual v)
norm2 kt = scalprod kt kt
normed kt = (1/sqrt(norm2 kt)) *> kt
...

Nous pouvons à présent faire des calculs "symboliques" (mais concrètes !)

psi = normed (2*>ket B0 <-> 7*>ket B1)
show (norm2 psi))   -- pour l'affichage, si on le veut

etc.

Si on ajoute à l'instantiation Oscil du substrat le bracket pour:

bracket (X x) (N 0) = exp(-x*x/2)  -- f. d'Hermite d'ordre 0

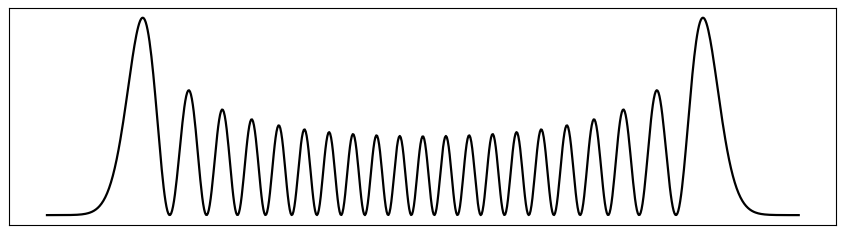avec 10 min de travail on peut déduire les récurrences pour $\braket{x}{n}$, et sans d'autres ingrédients trouver la distribution probabiliste spatiale (le carré de la fonction d'onde) pour l'oscillateur, niveau quelconque.

(Pour l'enseignement, l'approche algébrique est plus commode, facile et instructive que les solution de l'équation de Schrödinger, détestée par les étudiants).

Opérateurs

Ce modèle, comme tout autre, doit permettre faire des calculs numériques. Nous savons faire les superpositions, ainsi que calculer les produits scalaires. Il faut encore :

Transformer les états. L'évolution est une transformation ! En général, une transformation est une superposition de dyades élémentaires. Une dyade c'est le produit tensoriel : $\dyade{\phi}{\psi}$. Tout opérateur peut être écrit comme $A = \sum_{i,j}{a_{ij} \dyade{\alpha_i}{\alpha_j}}$.

Il faut savoir construir les états (et les opérateurs) des systèmes composites. Faire, en général, des produits tensoriels n'est pas évident, et si la dimension de l'espace des états est infinie (en physique : presque toujours... les qubits sont des exceptions), les mathématiques sous-jacentes peuvent être intraitables.

Il faut faire des exemples concrets. Nous allons montrer des "circuits quantiques" par ex. le mécanisme de Deutsch, et nous allons montrer comment développer la théorie des perturbations pour l'oscillateur anharmonique, avec le Hamiltonien $H = H_0 + V(x) = p^2/2 + x^2/2 + \lambda x^4$.

Ce qui est intéressant, si on sait comment faire $\dyade{\phi}{\psi}$, on sait comment faire le produit tensoriel de deux kets, $\ket{\phi}\ket{\psi}$, ce sont des objets (math et info) homologues. Et ainsi, nous forçons l'ordinateur, à implémenter un théorème en géométrie abstraite (ou en analyse fonctionnelle) – l'isomorphisme entre le produit $W\otimes V^{*}$, et les applications linéaires : $V \to W$.

Ceci est une définition naturelle : $(\dyade{\phi}{\psi}) \ket{\chi} = (\braket{\psi}{\chi}) \ket{\phi}$. Notre construction est une directe transcription de cela en Haskell.

(dyad phi psi) phi = chi (dual psi) *> phi

avec des variantes concrètes, par ex. la projection sur les états de base :

$$ \dyade{\alpha}{\beta} \ket{\psi} = \braket{\beta}{\psi} \ket{\alpha} \quad \to $$

(warp alpha beta) psi = psi (axis beta) *> ket alpha

Dans notre style, les constructions qui correspondent aux inversions B0 ⇆ B1, la négation de la composante B1 (la matrice $\sigma_z$ de Pauli), et la matrice de Hadamard H :

$$ \begin{pmatrix}0 & 1\cr 1 & 0\cr\end{pmatrix} \qquad \begin{pmatrix}1 & 0\cr 0 & -1\cr\end{pmatrix} \qquad \frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1\cr 1 & -1\cr\end{pmatrix} $$

sont, avec prj alpha = warp alpha alpha : $\dyade{\alpha}{\alpha}$ :

qnot = warp B0 B1 <+> warp B1 B0
sigz = prj B0 <-> prj B1
had  = sqrt 0.5 *>(qnot <+> sigz)

Je souligne encore une fois : Les valeurs numériques dans la représentation classique n'ont aucun sens. En général, en physique, les valeurs numériques des composantes des vecteurs n'ont du sens que dans le cadre d'un système de coordonnées concret. Un vecteur est une entité "objective", indépendante du repère choisi, son changement ne modifie pas l'ontologie.

Mais dans la théorie quantique, c'est beaucoup plus tordu, puisque les composantes sont en principe non-mesurables et même incomparables. Aucun moyen de vérifier que deux états quantiques soient identiques...

Contrairement à la notation matricielle, la nôtre, considérablement plus "pauvre", est capable de traiter les espaces de dimension infinie, car demander la valeur d'une composante quelconque est simplement équivalent à demander la valeur $f(x)$ d'une fonction $f$ pour un $x$ : on applique la fonction.

Oscillateur encore

Définissons quelques opérateurs. Les projections, $\dyade{m}{n}$ sont universelles, on les a vues. Définissons l'opérateur de niveau (traditionellement il porte le nom $\hat N$, mais nous l'appelons "Level" : $L$, tel, que $L \ket{n} = n \ket{n}$.
Dans la base standard, il est $$ L = \sum_{m=0}^\infty {m \cdot \dyade{m}{m}}\,. $$ À cause de la somme infinie, un calcul effectif semble compromis. Mais quand $L$ agit sur un vecteur : $\ket{\psi} = L \ket{\phi}$, nous avons toujours un objet opaque, on ne peut "extraire" une valeur de l'intérieur que par l'opération de mesure : $\braket{m}{\psi} = \avg{m}{L}{\phi}$.

On force l'ordinateur à faire un peu de math... Le "sandwich" : $\avg{\phi}{A}{\psi}$ peut être compris comme $(\bra{\phi}{A}) \ket{\psi}$, sauf que l'opérateur agissant à gauche est conjugué Hermitien par rapport à l'original. En géométrie, les gens appellent cela le "pullback".

Si on a un opérateur $f$ agissant sur les éléments $x$: $f : x \to f x$ d'un espace vectoriel métrique, et si $u$ est la forme duale, telle que $(u\ x)$ est un scalaire, alors $f$ implique l'existence d'un $f^{+}$ tel, que $(f^{+} u) x = u (f x)$.

En Haskell, si ax, ax1 sont des axes, et psi – un ket, qui est un élément de l'espace dual, ayant un opérateur ax_Op dans l'espace des axes proche du substrat et des mesures concrètes – on peut "booster" cet opérateur (concrètement : son transposé !) op dans l'espace des kets

(op psi) ax = psi (ax_Op ax)

Ici : (ax_Level ax) (N n) = sc(n) * (ax (N n))
où sc est une abréviation qui fait d'un integer $n$ un nombre complexe.

et un "miracle survient", nous pouvons définir un opérateur dans l'espace de dimension infinie :

level psi = psi . ax_Level   -- (.) compose deux fonctions

On peut faire la même chose avec l'opérateur d'annihilation, $a$ tel que $a \ket{n} = \sqrt{n} \ket{n-1}$.
Ou : ($ a = \sum \sqrt{m}\dyade{m}{m-1}$).

ax_an ax (N n) = sqrt(sc n) * ax (N (n-1))
an = boost ax_an   -- boost = flip (.);  flip f x y = f y x

Systèmes composites, états tensoriels

Pour un système classique, l'espace des propriétés est un produit Cartésien des composantes, un "record" avec les attributs des parties. Dans la théorie quantique on forme les produits tensoriels, $\ket{\phi,\psi} \equiv \ket{\phi} \otimes \ket{\psi}$, noté aussi comme $\ket{\phi}\ket{\psi}$.

Pour les matrices c'est le produit de Kronecker ; pour M qubits : un objet avec $2^{M}$ éléments. Ici c'est une fonction de M paramètres... Nous aurons aussi besoin d'opérateurs agissant sur les M-vecteurs. Ceci devient intéressant quand on construit les superpositions des produits tensoriels, les états intriqués (entangled).

Voici "controlled-not" : "XOR" unitaire, reversible, sur 2 qubits ; essentiel pour tous les algorithmes quantiques, il change l'intrication entre les qubits. Sa sémantique est : Le second qubit est inversé SSI le premier est "1". (modulo conventions...) Son implémentation est délicate, et sa simulation classique souffre de l'inefficacité : son action prend du temps et décompose les états (il les mesure).

$$ \mathrm{cnot}(4 \times 4) = \begin{pmatrix} \mathrm{id_2} & 0\cr 0 & \mathrm{qnot}\end{pmatrix} $$

Mais, – un grain de sable pour la notation matricielle – dans la base de Hadamard : $$ \ket{+} = \sqrt{1/2}(\ket{0}+\ket{1})\,; \qquad \ket{-} = \sqrt{1/2}(\ket{0}-\ket{1}) $$ c'est le premier qubit qui "flippe", le second reste spectateur... La vision trop classique mène à la confusion.

Nous écrirons : cnot $= \dyade{00}{00} + \dyade{01}{01} + \dyade{10}{11} + \dyade{11}{10}$

En Haskell ce sera

(cnot kx ky) ax ay = r B0 id + r B1 qnot where
  r q op = prj q kx ax * op ky ay

C'est plus abstrait que la forme matricielle, mais pas de miracle : il faut choisir une base...

Cela nous servira à implémenter une "boîte noire" réalisant l'algorithme de Deutsch – une fonction $f(b)$ vérifiant si $f$ est une fonction telle que $f(B_0) \neq f(B_1)$ (identité), ou si c'est une fonction constante. Le procédé classique consiste à évaluer $f(B_0)\ \mathrm{XOR}\ f(B_1)$, si c'est vrai, $f$ est injective.

La solution ne peut être un boîtier $ 2 \to 1$ qubits, XOR n'est pas unitaire. Un qubit "en soi" ne peut disparaître. Il y aura un qubit de sortie supplémentaire, le "déchet" qui augmente l'entropie liée au calcul.
Le boîtier f est une généralisation du cnot, qui calcule $\ket{x}\ket{y} \to \ket{x} \ket{f(x) \oplus y}$

fcnot f kx ky ax ay = r B0 + r B1 where
  op B0 = id;  op B1 = qnot  -- la négation  1-qb
  r q = warp q q kx ax * op (f q) ky ay

Comme cnot, ce n'est qu'un modèle informatique. la fonction op est classique. Voici le code final, aux éléments ci dessus on ajoute encore des trivialités dans l'espace des axes.

deutsch f = \ax ay ->
  let ph = fcnot f (had (ket B0)) (had (ket B1))
      axwarp a b ax = ax a *> axis b
      axqnot = axwarp B0 B1 <+> axwarp B1 B0 
      axhad = axqnot <+> axwarp B0 B0 <-> axwarp B1 B1
  in  ph (axhad ax) ay

L'expression deutsch f (axis B0) arbitr donnera 1 pour la fonction constante, et 0 pour l'injective. Et vice-versa

Téléportation

Cette expérience sur le plan mathématique n'a rien de particulier. On construit un état imbriqué de trois qubits, deux connus, et un inconnu (le Captain Kirk). On effectue l'ensemble de mesures combinées, récupérant deux bits classiques, et ceci permet le reconstruction d'un Kirk'. Au vu de ce modèle, ainsi que d'un autre, nommé "dense coding", une conjecture est apparue : un qubit cache deux bits d'information classique
(et personne ne sait quel est le sens physique de cette affirmation... Il ne faut pas oublier que l'intrication est une ressource supplémentaire d'information "secrète").

Le côté intrigant de l'expérience est que Kirk et ensuite Kirk' peuvent se trouver à une distance quelconque, à condition que les deux qubits connus après leur entanglement se retrouvent loin l'un de l'autre.

Cependant, leur état quantique commun n'est pas et ne sera plus jamais le produit tensoriel de deux composantes. C'est tout, le calcul est assez ennuyeux...

Le premier cnot à droite produit l'état de Bell, intriqué, la paire dont un membre sera expédié loin : bell=(1/sqrt 2) *> (k0<*>k0 <+> k1<*>k1). Ceci n'est pas fait à la main, mais avec le circuit bell=cnot (had (ket B0) (ket B0).

L'autre qubit est intriqué avec $\varphi$ et les deux sont mesurés, fournissant un de quatre possibles résultats, (00) - (11) numérotés 0, 1, 2, et 3.

Le récepteur récupère cette information classique, et selon la valeur obtenue, applique une de quatre opérations : id, qnot, sigz, ou $\dyade{1}{0} - \dyade{0}{1}$ au qubit envoyé, et Kirk' prend les commandes.

Théorie des perturbations "paresseuse"

Oscillateur anharmonique

Il s'agit de résoudre l'équation de Schrödinger $ (H_0 + \lambda V)\ket{\psi} = E \ket{\psi}$, où $\lambda$ est un petit paramètre modifiant le Hamiltonien (opérateur d'énergie) ; le point de départ est : $ H_0\ket{\psi^{(0)}_k} = E^{(0)}_k \ket{\psi^{(0)}_k}$. On cherche les énergies, avec $V(x)=x^4$. Les énergies non-perturbées sont $E_k = \hbar\omega(k+1/2)$. Par la suite, oublions l'énergie du vide $1/2$, et choisissons $\hbar\omega=1$.
On connait la solution non-perturbée, les états $\ket{n}$ de l'oscillateur harmonique. C'est la base de presque tous les systèmes périodiques, et de la théorie des champs en particulier : les niveaux d'excitation dénotent les nombres de quanta (photons, etc.). On cherchera le développement en série :

$$ E = E^{(0)} + \lambda\cdot E^{(1)} + \lambda^2 \cdot E^{(2)} + \cdots = E^{(0)} + \lambda \overline{E}(\lambda) $$

et aussi les états perturbés, leurs éléments matriciels $\braket{k}{\psi^{(m)}} $.

$$ \ket{\psi} = \ket{\psi^{(0)}} + \lambda \ket{\psi^{(1)}} + \lambda^2 \ket{\psi^{(2)}} + \cdots = \ket{\psi^{(0)}} + \lambda \ket{\overline{\psi}(\lambda)} $$

On cherche une solution numérique ! (coeffs de la série en $\lambda$.

On cherchera la correction autour de l'état $\ket{0}$ ; $E^{(0)}=E_0$, et on pourra noter $\avg{k}{V}{m}=V_{km}$. Alors :

$$ V\ket{0}+\lambda V\ket{\overline{\psi}} = \overline{E}\ket{0}+(E_0 - H_0)\ket{\overline{\psi}} + \lambda \overline{E}\ket{\overline{\psi}}\,. $$
La cohérence de la normalisation demande $\braket{0}{\overline{\psi}}=0$, et les produits scalaires de l'équation ci-dessus avec $\bra{0}, \bra{k}$, donnent

$$ V_{00} + \lambda \avg{0}{V}{\overline{\psi}} = \overline{E}\,, \qquad \braket{k}{\overline{\psi}} = \frac{1}{E_0-E_k + \lambda \overline{E}} \big( V_{k0} + \lambda \avg{k}{V}{\overline{\psi}}\big)\,. $$

La première correction est $\ovl{E}^{0} = V_{00}$. Éliminons $\avg{k}{V}{\overline{\psi}} $ par la décomposition dans la base non-perturbée : $\avg{k}{V}{\ovl{\psi}} = \sum_m \avg{k}{V}{m}\braket{m}{\ovl{\psi}}$. On a :

$$ \c \ovl{E} = V_{00} + \lambda \sum_k V_{0k} \braket{k}{\overline{\psi}}\, , \\ \c \braket{k}{\overline{\psi}} = \frac{1}{E_0-E_k + \lambda \overline{E}} \Big( V_{k0} + \lambda \sum_m V_{km}\braket{m}{\overline{\psi}}\Big) $$

Voici deux équations couplées, pour $\ovl{E(\lambda)}$ et $\braket{m}{\ovl{\psi(\lambda)}}$. La séparation des degrés de $\lambda$ est pénible, mais elles constituent un algorithme co-récursif légitime.

Le modèle fonctionnel servira à calculer v k m = $V_{km}$, avec $V = x^4 = 1/4 \cdot(a+a^{+})^4$, puisque $x = 1/\sqrt{2}(a+a^{+})$. Cette forme est finie, avec un potentiel de degré 4, les seules contributions seront pour $|k-m| = 0, 2, 4$. L'élément matriciel est

v k m = 0.25*realPart((x . x . x . x) (ket (N m))(axis (N k)))
   where x = an <+> cr   -- Pas de termes imaginaires

Les inconnues seront des structures de données – séries infinies en $\lambda$:

data Ser a = a :> Ser a

Elles sont similaires aux listes, mais la multiplication, division, fonctions comme sqrt, etc., sont spécifiques. Si $u = u_0 + \lambda \tilde u = u_0 :> \tilde u$, la multiplication, et la division sont

(u0 :> uq) * v@(v0 :> vq) = u0*v0 :> (u0*:>vq + v*uq)
(u0 :> uq) / v@(v0 :> vq) = w0 :> wq where
     w0=u0/v0;  wq = (uq - w0*:>vq) / v

Le reste est le codage basé sur les formules ci-dessus, sans plus de "travail intellectuel"...

ebar = v 0 0 :> sum [v 0 k *:> psi k | k <- [2,4]]
psi k | k>0 = (v k 0 :> 
        sum [v k m *:> psi m | m <- [k-4,k-2 .. k+4]]) / 
            ((-k):>ebar)
      | otherwise = 0

et le travail est presque fini, sauf que le programme engendre 7 - 8 termes : [0.75, -2.625, 20.8125, -241.289, 3580.98, -63982.813 ...], et le ralentissement devient peu supportable, la complexité exponentielle de la double récursivité réclame ses droits... La solution est la mémoïsation paresseuse, les termes $\braket{k}{\psi}$ une fois calculés, seront stockés dans une liste auxiliaire, et récupérés sans plus de calcul. Voici le code final

psi k | k>0 = lpsi !! k   -- indexation, lpsi[k]
      | otherwise = 0 
lpsi = 0 : ps 1 where
   ps k = ((v k 0:>sum[v k m*>psi m|m<-[k-4,k-2..k+4]])/ 
          ((-k) :> ebar)) : ps(k+1)

Représentation fonctionnelle des objets quantiques