GPS, Tracking.

On a nos coordonnées. Et alors?...

Puisque je vous ai suggéré de faire un "devoir nomade", de vous promener à pied, à vélo, en voiture, par ex. de faire un parcours entre Caen et une autre ville, ou visiter un joli endroit, par ex. Ouistreham, Pointe du Siège :

... l'idée est de lancer un processus automatique, qui récupère périodiquement vos coordonnées, et qui stocke les résultats dans un fichier qui peut ensuite être affiché sur Google Maps, Mapnik, OSMarender ; un éditeur de cartes genre JOSM, etc. (Quelques uns de ces logiciels seront commentés plus tard.)

La première constatation, est que le nombre d'outils est exorbitant, des centaines de logiciels. Pour ceux qui en ont une certaine expérience/compétence, la seconde est que la plupart de ces logiciels (y compris payants) est de très mauvaise qualité... Dans ces circonstances l'usage des solutions professionnelles est avantageux, et ils évoluent rapidement.
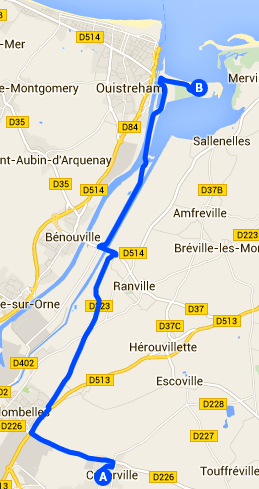
Voici le trajet entre ma maison et la Pointe du Siège, en voiture, avant la promenade à pied. Même si 98% d'utilisateurs de Google Maps considèrent le logiciels comme un service de visualisation interactive, nous pouvons faire mieux. Par exemple, exporter le contexte sous forme de lien.

Google peut stocker une nouvelle carte personnalisée, et depuis cette carte exporter nos données (le parcours) en format kml : un dialecte XML, directement affichable sous, par ex. Google Earth. Si on veux un format plus portable et succint, on peut le convertir en GPX, aussi XML, mais sans attaches aux détails Google.

Un logiciel commode pour la conversion entre plusieurs dizaines de formats est GSPbabel. L'essence d'un fichier GPX est la liste de coordonnées, 

...
<trkpt lat="49.189230000" lon="-0.267690000">
        <ele>0.000000</ele> </trkpt>
<trkpt lat="49.189120000" lon="-0.267750000">
        <ele>0.000000</ele> </trkpt>
<trkpt lat="49.189050000" lon="-0.267900000">
        <ele>0.000000</ele> </trkpt>
...
avec d'autres descriptions telles que les limites, la date, l'auteur, etc. Les formats Google, kml (Keyhole Markup Language), kmz, etc. sont plus compacts, pas la peine de baliser tous les points ; mais peuvent contenir d'autres objets, comme "Placemark", "HotSpot", etc., ainsi que ds données des capteurs spécifiques. Les fichiers représentant des parcours dynamiques, fait à l'aide des GPS et autres dispositifs, peuvent contenir des données comme la fréquence cardiaque d'un coureur.

L'acquisition des données par un GPS Android est relativement triviale. Vous avez (à travers les appels de getSystemService) l'accès à Location Manager, et vos applications peuvent simplement allumer le GPS et récupérer les coordonnées.

Même les applications Web, codées en javaScript peuvent le faire. Normalement le système doit contenir le fichier "manifest", avec, disons, <uses-permission android:name="android.permission.ACCESS_FINE_LOCATION" />. Dans ces circonstances, ce qui reste est l'appel périodique aux services, avec la fréquence souhaitée, par exemple routes les deux secondes. 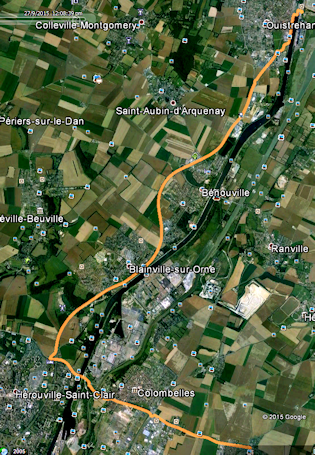On stocke les coordonnées, et à la fin de l'acquisition, on exporte un GPX (ou kml etc.). (Le fichier contient aussi les données horloge : <time> ... </time>, absentes de la simulation par Google Maps).

J'ai testé plusieurs applications, plusieurs sont pénibles à l'usage. Voici quelques unes qui marchent sans trop de soucis, mais SVP, testez les autres, et rapportez vos opinions dessus.

Pour l'affichage, on peut exploiter GMaps, Google Earth, ou GPX Viewer (Android), parmi d'autres. Plusieurs services (au moins une dizaine) en ligne utilisent les APIs Google, et combinent les tracks avec les cartes Google. Une autre approche fait le même avec les cartes OpenStreet Map (on le discutera prochainement).

Les mesures d'altitude (élévation) sont moins précises que les coordonnées horizontales, mais les rapports locaux, les différences relatives sont relativement bonnes. Exercice. Comment calculer les pentes du chemin tracé en GPX?

Comment trouver la distance entre deux points, ayant leurs coordonnées géodésiques? La formule simplifiée, sphérique, est connue depuis des siècles, mais la formule ellipsoïdale, de bonne précision, a été élaborée par Thaddeus Vincenty seulement en 1975...

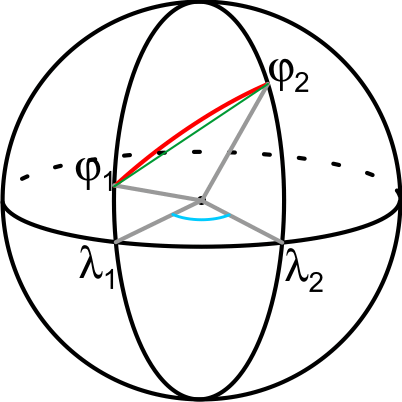
Commençons par le cas sphérique. Il est inutile d'essayer mémoriser une formule géniale qui vous donne la distance, l'essentiel est de comprendre l'idée, vous pourrez alors reconstruire la solution en quelques secondes. Étant données les coordonnées géodésiques \((\lambda,\varphi)\), il est facile de reconstruire les coordonnées cartésiennes : $$x = R\cos(\varphi)\cos(\lambda), y = R\cos(\varphi)\sin(\lambda), z = R \sin(\varphi)\,.$$ Ainsi nous aurons deux vecteurs : \(\vec{x}_1 = (x_1, y_1, z_1)\), et \(\vec{x}_2 = (x_2, y_2, z_2)\).

La longueur des deux est \(R\).

L'angle entre ces deux vecteurs satisfait la relation \(\cos(\alpha) = \vec{x}_1 \cdot \vec{x}_2 / R^2\). Si on cherche la distance la plus courte entre les points, cet angle est toujours entre 0 et 180°, et le cosinus suffit pour trouver cet angle. Ayant $$ \alpha = \arccos(\cos(\varphi_1)\cos(\lambda_1) \cdot \cos(\varphi_2)\cos(\lambda_2) \\ + \cos(\varphi_1)\sin(\lambda_1) \cdot \cos(\varphi_2)\sin(\lambda_2) \\ + \sin(\varphi_1) \cdot \sin(\varphi_2)) \\ = \arccos\left( \cos(\varphi_1)\cos(\varphi_2) \cos(\lambda_1-\lambda_2) + \sin(\varphi_1) \sin(\varphi_2)) \right)\,. $$ Ensuite, la distance vaut \( s = R \alpha \), et c'est tout.

La formule de Vincenty, de précision millimétrique, est itérative, pas trop longue, mais peu lisible. Il va de soi que pour les points voisins sur une trace GPX, la Terre est plate, et ce sont les irrégularités du terrain qui dominent. Par exemple – calculons la distance entre mon domicile et le bâtiment Sciences 3.

Avec ces données, la distance en vol d'oiseau donnée par le Grand Cercle sphérique est de 7774.5465 m.
Si la Terre était plate, pour calculer la distance, il faudrait uiliser le théorème de Pythagore, avec une correction : les méridians convergent vers le pôle. La "non-projection" équirectangulaire est équidistante verticalement, on peut prendre directement la latitude comme une coordonnée. Par contre, la longitude (ou la différence de longitudes) doit être pondérée par \(\cos(\varphi)\). Prenons la latitude moyenne, \(\varphi_m = 0.5 (\lambda_1+\lambda_2)\).

La formule est : \(d=R \sqrt{(\varphi_2-\varphi_1)^2 + [\cos(\varphi_m)\cdot(\lambda_2-\lambda_1)]^2}\). Cela donne 7774.5473 m. La précision si excellente est un peu accidentelle, mais la courbure est négligeable.

Pour le tracking habituel, avec les mesures prises quelques fois par minute, les différences entre les modèles de la Terre sont complètement dérisoires.

Il ne faut se tromper : si quelqu'un pense que j'ai vraiment calculé la distance horizontale entre Cuverville et le Bd. Maréchal Juin avec la précision millimétrique, c'est faux. D'abord, le rayon moyen de la Terre est OK, mais pas avec la précision d'un mètre.

Le rayon géocentrique satisfait la formule $$ R(\varphi) = \sqrt{\frac{(a^2 \cos\varphi)^2 + (b^2 \sin\varphi)^2} {(a \cos\varphi)^2 + (b \sin\varphi)^2}}\,. $$ Et le paramétrage WGS84 donne la valeur 6365926.3 m. Les rapports relatifs restent valables, mais la distance est...: 7768.34 m, 6 mètres de différence.

Ceci termine - pour l'instant - cette section,mais il est possible que nous y reviendrons, afin de faire quelques exercices.

De toute façon il nous faudra programmer un peu pour Android, et une partie du travail pourra se faire par Javascript integré dans une page Web...