Introduction à la cartographie
Répétons que l'essence de ce cours n'est pas l'Informatique Géographique, mais une introduction concernant les données utilisées et leur traitement dans le contexte géographique me semble indispensable. Si vous voulez une ou plusieurs cartes dans un format quelconque, les ressources Internet sont infinies... Cependant pour le "nomadisme" en général, l'essentiel est que les gens souvent n'importent plus des cartes, mais les font chez eux. De plus, ils ont besoin souvent de formats différents pour la même zone.
-
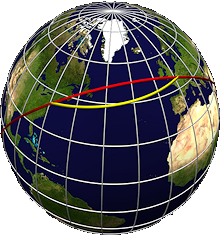 Pour la navigation (maritime, aérienne...) on peut vouloir que la "ligne de cap" (loxodromie) soit une ligne droite, ou que la ligne plus courte (géodésique ; grand cercle ; orthodromie) soit droite. (La loxodromie n'est pas la plus courte, c'est une spirale qui s'enroule autour du pôle.)
Pour la navigation (maritime, aérienne...) on peut vouloir que la "ligne de cap" (loxodromie) soit une ligne droite, ou que la ligne plus courte (géodésique ; grand cercle ; orthodromie) soit droite. (La loxodromie n'est pas la plus courte, c'est une spirale qui s'enroule autour du pôle.)
-
Ou, que les distances depuis la position de l'utilisateur soient préservées (on peut chercher le port le plus proche).
-
Dans d'autres cas nous voudrions préserver les rapports entre les surfaces : les zones grandes seraient grandes, et petites : petites, contrairement à par ex. Mercator, qui gonfle le Groenland par un facteur de 16 par rapport à l'Afrique.
-
Parfois - comme sur le dessin ci-dessus - nous voulons une représentation "réaliste", montrant une image de la Terre vue de l'espace (c'est une projection dite orthographique).
-
Finalement, pour des raisons historiques / politiques, chaque pays définit des projections dites officielles, qui doivent obligatoirement représenter le pays entier, ou ses fragments, à des buts administratifs. Les détails changent de pays en pays, car les critères des choix ne sont plus discutables... Parfois c'est la volonté de minimiser les distortions globalement, parfois c'est culturel (certains Australiens exigent à ce que en haut de la carte on trouve le pôle sud).
Toutes ces transformations sont hautement non-linéaires, et convertissent les géométries selon des formules assez compliquées, mais avant cette conversion, on peut poser plusieurs questions, par exemple :
Comment je sais que ma position actuelle est : Lat. N. 49°11'21.551'', et Lon W. 0°16'03.09'' (ma maison. Localisez mon adresse, SVP, c'est votre premier devoir obligatoire) ? Comment mon GPS attribue les coordonnées géodésiques aux points sur la Terre?
La première chose à faire est d'établir un modèle du globe terrestre, proche de la réalité, mais représentable mathématiquement. Ceci n'est pas trivial, et change avec le temps. Nous décrirons le plus populaire, officiellement utilisé par le système GPS.
WGS84
Ce système géodésique des années '80 a été modifié encore en 2004, et cela probablement continuera. La base (avant toutes les distorsions) est une ellipsoïde de révolution, placée dans un système Cartésien géocentrique. La Terre inclut les océans et l'atmosphère, et son centre est considéré connu avec une précision meilleure que 2 cm.
L'axe Z pointe vers le pôle Nord conventionnel (1984; l'axe de rotation de la Terre bouge...), avec précision de 0.005". L'axe X réside sur le plan qui passe par le centre et est orthogonal à Z. Sa direction est le méridien zéro [IERS Reference Meridian (IRM)]. Il coïncide avec le méridien zéro BIH (Bureau International de l'Heure, '1984). Il passe 102.5 m (5.3 secondes) du méridien historique de Greenwich.
Les paramètres de l'ellipsoïde sont par définition
-
Le demi grand axe : a = 6 378 137.0 m
-
L'aplatissement \(f = (a-b)/a\) = 1/298.257 223 563
Donc, par calcul :
-
Le demi petit axe b = 6 356 752.314 245 179 497 563 967 m
-
Première excentricité \(e=\sqrt{\frac{a^2-b^2}{a^2}}\) = 0.081 819 190 842 622
Une petite digression... Dans les Sciences de la Nature, où on mesure des entités physiques, un paradoxe est inévitable : la nécessité de figer une valeur en toute indépendance desdites mesures. Par exemple, la vitesse de la lumière, absolument essentielle pour la connexion entre le temps et les distances, critique pour le fonctionnement des GPS, vaut 299 792 458 m/s, et c'est une valeur exacte, établie par BIPM (Bureau Int. des Poids et Mesures) en 1983. Aucune expérience, qui change de précision, ou ajuste une micro-erreur systématique, ne changera cette valeur. Alors, qu'est-ce que change, si on obtient des nombres différents?
La réponse est : on modifie la définition du mètre... Cette entité est dérivée, associé à une seconde, définie comme valeur fondamentale : la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les niveaux hyperfins F=3 et F=4 de l’état fondamental \({}^6S_{1/2}\) de l’atome de césium 133 au repos (température zéro).
Revenons au système géodésique...
L'ellipsoïde est ensuite modifiée par l'ajout de plusieurs milliers de harmoniques sphériques. La géoïde résultante a la précision meilleure que 100 km par rapport à la Terre physique. Bien sûr, ce nombre n'a rien à voir avec la précision de GPS.
Tout le système est corrigé en permanence, il faut tenir compte du mouvement des plaques terrestres, des effets relativistes (dé-synchronisation des horloges à cause de la vitesse des satellites et de la force gravitationnelle), fluctuations des marées...
Projections cartographiques classiques.
Les données en format vectoriel (shapefiles, XML [OpenStreetMap]), etc., qui doivent être visualisées, sont typiquement stockées dans des coordonnées "naturelles" : longitude / latitude, ou \(\large(\lambda,\varphi)\), avec la latitude mesurée depuis l'équateur, sud : valeurs négatives, longitude depuis le méridien zéro, valeurs négatives à l'ouest.
Si on considère simplement que \(\lambda\) est la coordonnée "x", horizontale, et \(\varphi\) : "y", verticale, on obtient la carte dite équirectangulaire, qui n'est pas considérée comme une projection cartographique. On publie des graphiques géométriques dans ces coordonnées, et aussi des cartes - images satellite, qui peuvent être utilisées pour la texturation des objets 3D.
Concernant la visualisation d'une shapefile avec les contours des pays et des continents, faisons l'expérience interactive en Python [worldtab.py]. / ... /
Observons que la distorsion des zones polaires est très grande, voire extrémale : le pôle (point) devient une ligne, la transformation de la sphère en rectangle (plus exactement : en cylindre) engendre des singularités. Alors, à titre d'exemple, affichons la sphère (ou une partie), avec le pôle au centre, par une variante de projection azimutale. Ceci est le premier exemple d'une transformation non-linéaire, seulement comme un petit exercice mathématique (en fait, deux exercices complémentaires).
Localement, autour du pôle (sud ou nord), la latitude est proportionnelle au rayon, non pas à la coordonnée cartésienne y. Dans ces circonstances, la transformation des objets géométriques (lignes, ou paires de points) est la suivante :
$$ r = C \cdot \varphi \\
\alpha = \lambda\,,$$
où il faut choisir la constante C de manière à obtenir le graphique de taille convenable (Matplotlib est capable d'ajuster cela automatiquement). La variable \(\alpha\) représente l'angle azimutal. Ensuite on retourne aux coordonnées cartésiennes :
$$ x = r\cdot \cos(\alpha)\,; \quad y=r \cdot \sin(\alpha)\,.$$
et c'est tout, on lance la même boucle qui affiche les lignes.
Par contre, la projection d'une image suit une autre algorithmique, et ceux qui veulent jouer avec un minimum d'imagerie sur leur équipement informatique, doivent connaître l'essentiel. Les pixels ne peuvent être traités comme des entités géométriques genre lignes ou points dans des shapefiles. Leurs coordonnées (indices) sont entières, séquentielles, pixels ..., (n,0), (n,1), (n,2), ..., (n,M-1), (n+1,0), (n+1,1), ... . Si on transforme ces indices en coordonnées, par ex. \((n,m) \to (\frac{n}{N}\cdot 2\pi - \pi ,\frac{m}{M}\cdot \pi - \pi/2 )\), la transformation non-linéaire peut dédoubler quelques pixels, ou/et laisser des trous. La stratégie est donc la suivante :
-
On parcourt tous les pixels de l'image cible, après avoir alloué un tableau convenable dans la mémoire.
-
Pour chaque (x,y), indices entières identifiant ce pixel, on effectue la transformation inverse vers la source (donc vers \(\lambda, \varphi\) dans notre contexte). On récupère le pixel-source, et on transfère sa couleur sur le pixel-cible. Ainsi on est sûr que la cible ne présentera pas des incongruités topologiques. Par contre, si la qualité est importante, puisque les valeurs des coordonnées dans la source ne sont pas entières, il faudra peut-être interpoler. Ceci ne sera pas traité ici, sauf si vous me demandez.
Pour notre exercice "radial", la stratégie est la suivante. On alloue un tableau carré, de N pixels de côté. L'espace 0 - N-1 correspond à la latitude \(-\pi/2 \to \pi/2\), éventuellement moins, si on veut tronquer l'original. Mais \(-\pi/2\) doit se trouver au centre, autour de la position N/2. La longitude restera angulaire. Pour le pixel (x,y) cible, d'abord on normalise les valeurs, afin d'éliminer la dépendance de la taille de l'image cible. Que le rayon maximal soit égal à \(\pi\), d'un pôle vers l'autre
$$x \leftarrow (x/N - 1/2)\cdot 2\pi\,; y \leftarrow (y/N - 1/2)\cdot 2\pi\,. \quad
\mathrm{Ensuite} \quad \varphi=\sqrt{x^2+y^2} - \frac{\pi}{2}\,.$$
Ceci est notre latitude - source qui doit encore être converti en indice - source. Ceci est une source d'erreurs persistantes, car il ne faut pas oublier que dans l'imagerie l'axe des Y pointe vers le bas. Pour les données vectorielles ce phénomène n'a pas eu lieu.
Donc, en fait, la latitude/numéro de ligne dans l'image-source, si la hauteur de l'image est H, vaut
$$
Y = H - \sqrt{x^2+y^2}\cdot H/\pi
$$
 La longitude réduite aux coordonnées pixel est \(\alpha = \arctan2(y,x)\,; X = (\alpha +\pi)\cdot L/2\pi\), si la largeur est L (ceci doit être égale à 2H, mais la source peut être déformée).
La longitude réduite aux coordonnées pixel est \(\alpha = \arctan2(y,x)\,; X = (\alpha +\pi)\cdot L/2\pi\), si la largeur est L (ceci doit être égale à 2H, mais la source peut être déformée).
Voici le résultat [worldimg]. La technique présentée souffre de lenteur (et si on ajoute l'interpolation des couleurs, afin d'améliorer la qualité, ce sera pire) : Python, comme langage interprétée, où les boucles et accès aux structures indexées consomment trop de temps. En C# (ou Java), éventuellement en C/C++ ceci serait quelques dizaines de fois plus rapide.
Ceci dit, répétons : notre objectif est de montrer des codes raisonnables, faciles à faire, rapides à déboguer. Je vous montrerai très prochainement comment accéler le processus en Python, grâce à la programmation vectorielle avec numpy.
Projections ; classification selon les schémas 3D
Projections cylindriques
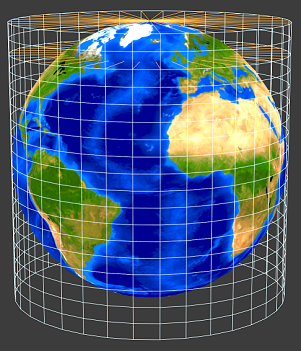 Le schéma équirectangulaire, ou "Plate carrée" peut être considéré comme une sorte de projection cylindrique triviale. Les lignes de projection partent de l'axe \(Z\). L'image est sur la surface cylindrique. La plate carrée s'appelle aussi équidistante (ce qui est ambigu). Les distances sont conservées sur l'équateur, et le long des méridiens, ce qui dans le jargon lui a donné le nom d'aphylactique.
Le schéma équirectangulaire, ou "Plate carrée" peut être considéré comme une sorte de projection cylindrique triviale. Les lignes de projection partent de l'axe \(Z\). L'image est sur la surface cylindrique. La plate carrée s'appelle aussi équidistante (ce qui est ambigu). Les distances sont conservées sur l'équateur, et le long des méridiens, ce qui dans le jargon lui a donné le nom d'aphylactique.
Si on fait la projection perpendiculaire à l'axe \(Z\), comme à droite, on obtient une autre projection cylindrique, où la hauteur est proportionnelle au sinus : \(x=\lambda\,; y=\sin(\varphi)\).
C'est la projection cylindrique de Lambert, qui est équivalente, c'est-à-dire, conserve les aires (surfaces), même si les proportions deviennent fausses. On peut avoir l'impression que toute cette richesse de projections, qui sont parfois similaires, est inutile, et dérangeante. D'accord. Expliquez cela aux producteurs des ordinateurs, voitures, fromages... Toute cette richesse est inutile.
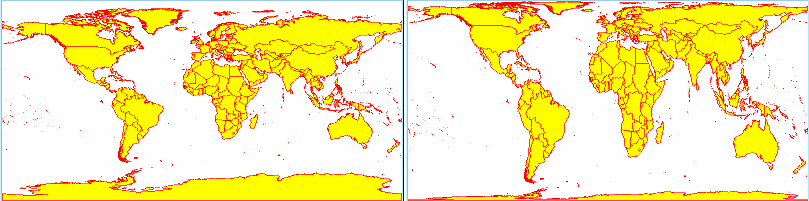
Voici la différence entre les formes équi-rectangulaire (à gauche) et Lambert cylindrique. Le trait commun de ces projections est la distorsion des zones polaires (où typiquement on utilise la projection azimutale).
L'exemple le plus classique et vénérable, est celui de la projection de Mercator (1512 - 1594), conçue autour de 1569, qui se caractérise par le fait que toutes les loxodromies ("rhumb lines"), les lignes qui coupent les méridiens sous un angle constant, sont droites. C'est une projection conforme, et je vous ai déjà montré sa forme.
La direction constante facilite la navigation, même si les loxodromies ne sont pas des lignes les plus courtes (ne sont pas des grands cercles, ou géodésiques) ; ceci n'était pas tellement important à l'époque des voiliers avec la longitude mesurée mal, à cause d'impossibilité d'avoir des horloges éloignés synchronisés en permanence.
Les projections cylindriques ne sont pas obligatoirement "verticales".
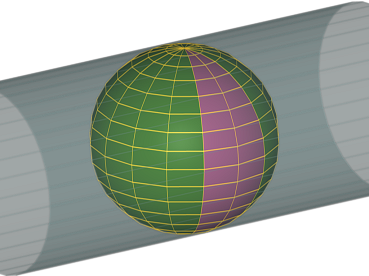 Ceci est le schéma de l'UTM : Universal Transverse Mercator capable de rendre de manière raisonnable les zones polaires et proches, ce qui la distingue du Mercator "classique". Cependant comme une projection globale elle est peu utile, les distorsions frappent les zones éloignées du méridien central.
Elle est utilisée souvent (parfois elle est officielle, par ex. aux États Unis, et par l'Otan). On divise la sphère en 120 zones, et on applique l'UTM à chaque zone. Les standards prévoient aussi 2 projections stéréographiques pour les zones polaires. Cette dernière est une projection azimutale, mais conforme (non pas photographique).
Ceci est le schéma de l'UTM : Universal Transverse Mercator capable de rendre de manière raisonnable les zones polaires et proches, ce qui la distingue du Mercator "classique". Cependant comme une projection globale elle est peu utile, les distorsions frappent les zones éloignées du méridien central.
Elle est utilisée souvent (parfois elle est officielle, par ex. aux États Unis, et par l'Otan). On divise la sphère en 120 zones, et on applique l'UTM à chaque zone. Les standards prévoient aussi 2 projections stéréographiques pour les zones polaires. Cette dernière est une projection azimutale, mais conforme (non pas photographique).

Projections coniques
Ce schéma est particulièrement utile dans les zones "tempérées", par exemple l'Europe, ou mieux, les fragments de l'Europe.
Comme avec les projections cylindriques, "être conique" ne précise pas tous les détails, il faut y ajouter d'autres éléments.
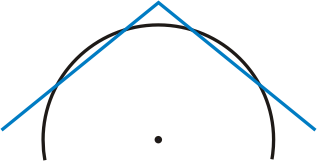 Si le cône est tangent à la sphère, un parallèle (l'isomètre central) et son voisinage est rendu fidèlement, plus loin les écarts augmentent. Mais on peut, comme à gauche, prévoir une configuration sécante, qui est exacte sur deux méridiens, et la zone entre les deux est assez correcte.
Si le cône est tangent à la sphère, un parallèle (l'isomètre central) et son voisinage est rendu fidèlement, plus loin les écarts augmentent. Mais on peut, comme à gauche, prévoir une configuration sécante, qui est exacte sur deux méridiens, et la zone entre les deux est assez correcte.
La projection officielle en France (depuis le décret du 26 décembre 2000) est le Lambert conique conforme, dite Lambert 93. Elle utilise deux parallèles sécants (automécoïques) : 44° et 49° (N), et le méridien de référence est 3° (E). Cette projection est liée au système géodésique RGF93, presque identique au paramètrage dans WGS84... Paradoxalement, elle n'est pas utilisée trop fréquemment à cause des inexactitudes. Pour y remédier, le décret 2006-272 a entériné la création de 9 projections coniques conformes sécantes, couvrant 9 zones du nord au sud...
Cette information (Wikipédia) est donc relativement récente. Le monde bouge ! En quoi cela vous concerne?
- On aura toujours besoin de gens capable de concevoir et de coder nouvelles cartes.
- La création des logiciels de géolocalisation, du rendu GPS, de navigation maritime, etc., a beaucoup d'avenir. [Et avant que cette calamiteuse initiative Européenne "Galileo" ne soit opérationnelle (espérons qu'avant votre retraite...), plusieurs normes changeront].
Classification des projections selon l'invariance
La richesse de solutions cartographiques est le résultat des objectifs des utilisateurs qui sont différents. Ainsi on a d'autres schémas de conception des projections. Ceci nous sera indispensable afin de comprendre les formules mathématiques utilisées, et donc pouvoir les coder. Il ne suffit pas de dire "projection azimutale", il existe au moins trois catégories : orthographique (vue), stéréographique et gnomonique.
La plupart de projections dérivées des cylindriques, appelées pseudo-cylindriques gardent une certaine fidélité concernant les distances relatives sur les parallèles (lignes horizontales), mais les parallèles subissent des retrécissements polaires quelconques ; ainsi il est plus facile d'adapter certaines propriétés d'invariance.
On veut d'habitude qu'une projection préserve quelque chose, parfois sur le plan intuitif / visuel, parfois dans le domaine algorithmique. Ceci impose des contraintes très fortes sur les formules. Nous aurons besoin d'un peu d'analyse mathématique. Pour commencer, les projection planaires, azimutales, conservent les directions émanant du centre. Elles peuvent également préserver les distances de ce centre (mais aucune autre).
Grâce à cela c'est la projection très utile dans la navigation maritime, surtout quand on a des problèmes et il faut prendre vite quelques décisions concernant la route...
Projections équivalentes.
Ces projections préservent les aires des zones. Sur un plan Cartésien, un élément surfacique \(dS\) est égal (sa valeur numérique, l'aire différentielle) à \(dx\cdot dy\). On voit donc que la carte équirectangulaire n'est pas équivalente, car \(d\lambda\cdot d\varphi\) n'est pas un élément surfacique sur la sphère.
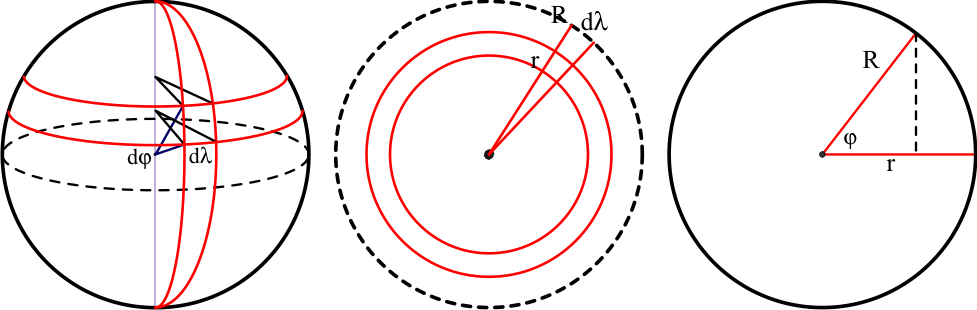 Le dessin central est la vue polaire, et le droit : équatoriale. On voit que le rayon \(r\) du parallèle à la latitude \(\varphi\) est \(r=R\cos(\varphi)\), dépend de la latitude. Donc, la longueur du segment horizontal sera \(R\cos(\varphi)d\lambda\). Par contre, le segment vertical a toujours la longueur \(R d\varphi\). Donc, \(dS = R^2 \cos(\varphi) d\lambda \cdot d\varphi\). Dans l'avenir nous prendrons typiquement \(R=1\).
Si on effectue une transformation \(x=x(\lambda,\varphi)\) et \(y=y(\lambda,\varphi)\), où \((x,y)\) sont considérées cartésiennes, \(dS = dx dy\). La transformation de l'élément surfacique est proportionnelle au Jacobien de la transformation (un minimum de connaissance de mathématiques s'impose...)
Le dessin central est la vue polaire, et le droit : équatoriale. On voit que le rayon \(r\) du parallèle à la latitude \(\varphi\) est \(r=R\cos(\varphi)\), dépend de la latitude. Donc, la longueur du segment horizontal sera \(R\cos(\varphi)d\lambda\). Par contre, le segment vertical a toujours la longueur \(R d\varphi\). Donc, \(dS = R^2 \cos(\varphi) d\lambda \cdot d\varphi\). Dans l'avenir nous prendrons typiquement \(R=1\).
Si on effectue une transformation \(x=x(\lambda,\varphi)\) et \(y=y(\lambda,\varphi)\), où \((x,y)\) sont considérées cartésiennes, \(dS = dx dy\). La transformation de l'élément surfacique est proportionnelle au Jacobien de la transformation (un minimum de connaissance de mathématiques s'impose...)
\(dS = dx dy = \left|\begin{array}{cc}
\frac{\partial x}{\partial \lambda} & \frac{\partial x}{\partial \varphi} \\
\frac{\partial y}{\partial \lambda} &
\frac{\partial y}{\partial \varphi}
\end{array}\right| d\lambda d\varphi =
\left( \frac{\partial x}{\partial \lambda}\cdot \frac{\partial y}{\partial \varphi} -
\frac{\partial x}{\partial \varphi} \cdot \frac{\partial y}{\partial \lambda} \right) d\lambda d\varphi\)
Ceci signifie qu'une projection est équivalente si \(\frac{\partial x}{\partial \lambda}\cdot \frac{\partial y}{\partial \varphi} -
\frac{\partial x}{\partial \varphi} \cdot \frac{\partial y}{\partial \lambda} = \cos(\varphi)\) (modulo une constante multiplicative qulconque ; le facteur global d'échelle n'a pas d'importance).
On voit clairement que la projection cylindrique de Lambert, avec \(y=\sin(\varphi)\) est équivalente.
Projections équidistantes
Il n'y en a pas beaucoup, et les universellement équidistantes n'existent pas. On peut toujours demander la préservation des distances le long d'une direction (ou, comme dans le cas azimutal, d'un point privilégié). Par exemple, si on choisit les méridiens, le critère est simple : \(\left(\frac{\partial x}{\partial \varphi}\right)^2 + \left(\frac{\partial y}{\partial \varphi}\right)^2 = 1\). Ici la plate-carrée est équidistante.
Projections conformes.
C'est une catégorie très importante, ces transformation préservent les angles, et donc localement les formes (deux lignes proches parallèles seront parallèles, et perpendicularité est aussi invariante, quelle que soit l'orientation des lignes.). Les contraintes mathématiques sont intuitives, mais un peu délicates, pas faciles pour les gens qui n'aiment pas la géométrie différentielle... Un rectangle sur la sphère : \((d\lambda,d\varphi)\) est transformé en rectangle, et les échelles des parallèles et des méridiens sont localement égales. Les éléments horizontaux et verticaux de la graticule restent perpendiculaires.
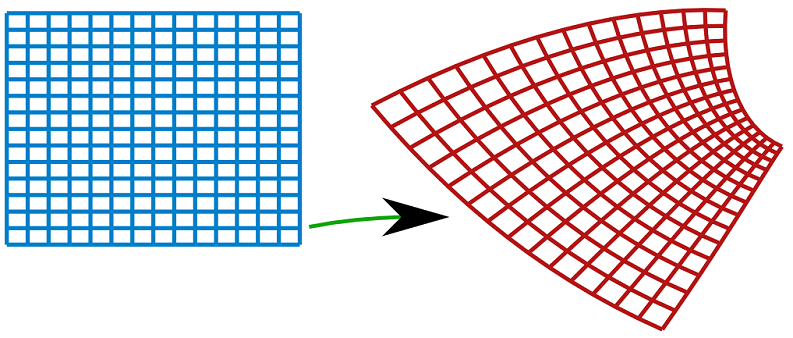
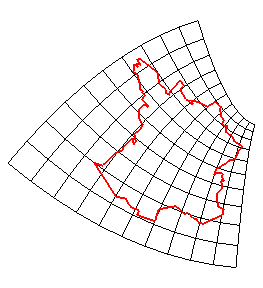 (La projection à gauche est similaire à Lambert conique conforme, utilisé officiellement pour la France).
Digression. Une observation "sociologique". Parmi une soixantaine de pages Web qui parlent de projections conformes, peut-être une ou deux contiennent des informations sérieuses (mathématiquement correctes et complètes, et pratiquement utiles : constructives, et pas trop difficiles)... Et pourtant, ce n'est aucune magie.
Si les angles sont conservés, alors un petit carré doit rester carré. Localement, modulo corrections d'ordre supérieur, le carré peut subir une rotation et une dilatation, c'est tout. Mais on ne doit pas utiliser directement les coordonnées \((\lambda,\varphi)\), car le "carré" implique l'usage des distances. Or, \(d\varphi\), la distance verticale est OK, mais \(d\lambda\) – non, la longueur du segment \(d\lambda\) se retrécit quand \(\varphi\) grandit, donc introduisons \(d\bar{\lambda} = d\lambda\cdot\cos(\varphi)\).
En général, la transformation sera conforme, si la matrice de Jacobi J :
(La projection à gauche est similaire à Lambert conique conforme, utilisé officiellement pour la France).
Digression. Une observation "sociologique". Parmi une soixantaine de pages Web qui parlent de projections conformes, peut-être une ou deux contiennent des informations sérieuses (mathématiquement correctes et complètes, et pratiquement utiles : constructives, et pas trop difficiles)... Et pourtant, ce n'est aucune magie.
Si les angles sont conservés, alors un petit carré doit rester carré. Localement, modulo corrections d'ordre supérieur, le carré peut subir une rotation et une dilatation, c'est tout. Mais on ne doit pas utiliser directement les coordonnées \((\lambda,\varphi)\), car le "carré" implique l'usage des distances. Or, \(d\varphi\), la distance verticale est OK, mais \(d\lambda\) – non, la longueur du segment \(d\lambda\) se retrécit quand \(\varphi\) grandit, donc introduisons \(d\bar{\lambda} = d\lambda\cdot\cos(\varphi)\).
En général, la transformation sera conforme, si la matrice de Jacobi J :
\(\left(\begin{array}{c}dx \\ dy \end{array}\right) =
J \cdot \left(\begin{array}{c}d\bar{\lambda} \\ d\varphi \end{array}\right)\,,\quad\) où
\(\quad J = \left(\begin{array}{cc}
\frac{\partial x}{\partial \bar{\lambda}}& \frac{\partial x}{\partial \varphi} \\
\frac{\partial y}{\partial \bar{\lambda}} &
\frac{\partial y}{\partial \varphi}
\end{array}\right)\,\)
où \(\frac{\partial P}{\partial \bar{\lambda}} = \frac{\partial P}{\partial \lambda} \cdot \frac{1}{\cos(\varphi)}\),
est localement la matrice de rotation fois un facteur scalaire \(s(\lambda,\varphi)\) d'échelle. Mais la forme de cette matrice est connue de tous :
\(\left(\begin{array}{cc}
\frac{\partial x}{\partial \bar{\lambda}}& \frac{\partial x}{\partial \varphi} \\
\frac{\partial y}{\partial \bar{\lambda}} &
\frac{\partial y}{\partial \varphi}
\end{array}\right) = s(\lambda,\varphi) \times
\left(\begin{array}{cc}
\cos(\alpha) & -\sin(\alpha) \\
\sin(\alpha) & \cos(\alpha) \end{array}\right)\).
Nous avons donc deux équations, équivalentes aux conditions "croisées" de Cauchy-Riemann :
\(\frac{\partial x}{\partial \lambda} = \frac{\partial y}{\partial \varphi} \cdot \cos(\varphi)\,,
\qquad
\frac{\partial x}{\partial \varphi} \cdot\cos(\varphi) = - \frac{\partial y}{\partial \lambda}\,.\)
[Digression mathématique. Ces conditions appartiennent au "monde" des fonctions analytiques des variables complexes, ce qui a priori est loin du domaine géographique. Cherchez "conformal mapping" sur le Web. Toute transformation conforme est une fonction analytique d'une variable complexe \(x + i y = F(\bar{\lambda}+ i \varphi)\)].
Nous passerons à présent aux exemples concrets, mais jetez un coup d'oeil sur une jolie applet de H.J. Bortolossi (Institut de Mathématiques, Université de Rio de Janeiro, Brésil) sur la page suivante.
 Pour la navigation (maritime, aérienne...) on peut vouloir que la "ligne de cap" (loxodromie) soit une ligne droite, ou que la ligne plus courte (géodésique ; grand cercle ; orthodromie) soit droite. (La loxodromie n'est pas la plus courte, c'est une spirale qui s'enroule autour du pôle.)
Pour la navigation (maritime, aérienne...) on peut vouloir que la "ligne de cap" (loxodromie) soit une ligne droite, ou que la ligne plus courte (géodésique ; grand cercle ; orthodromie) soit droite. (La loxodromie n'est pas la plus courte, c'est une spirale qui s'enroule autour du pôle.)
 La longitude réduite aux coordonnées pixel est \(\alpha = \arctan2(y,x)\,; X = (\alpha +\pi)\cdot L/2\pi\), si la largeur est L (ceci doit être égale à 2H, mais la source peut être déformée).
La longitude réduite aux coordonnées pixel est \(\alpha = \arctan2(y,x)\,; X = (\alpha +\pi)\cdot L/2\pi\), si la largeur est L (ceci doit être égale à 2H, mais la source peut être déformée).
 Le schéma équirectangulaire, ou "Plate carrée" peut être considéré comme une sorte de projection cylindrique triviale. Les lignes de projection partent de l'axe \(Z\). L'image est sur la surface cylindrique. La plate carrée s'appelle aussi équidistante (ce qui est ambigu). Les distances sont conservées sur l'équateur, et le long des méridiens, ce qui dans le jargon lui a donné le nom d'aphylactique.
Le schéma équirectangulaire, ou "Plate carrée" peut être considéré comme une sorte de projection cylindrique triviale. Les lignes de projection partent de l'axe \(Z\). L'image est sur la surface cylindrique. La plate carrée s'appelle aussi équidistante (ce qui est ambigu). Les distances sont conservées sur l'équateur, et le long des méridiens, ce qui dans le jargon lui a donné le nom d'aphylactique.

 Ceci est le schéma de l'UTM : Universal Transverse Mercator capable de rendre de manière raisonnable les zones polaires et proches, ce qui la distingue du Mercator "classique". Cependant comme une projection globale elle est peu utile, les distorsions frappent les zones éloignées du méridien central.
Elle est utilisée souvent (parfois elle est officielle, par ex. aux États Unis, et par l'Otan). On divise la sphère en 120 zones, et on applique l'UTM à chaque zone. Les standards prévoient aussi 2 projections stéréographiques pour les zones polaires. Cette dernière est une projection azimutale, mais conforme (non pas photographique).
Ceci est le schéma de l'UTM : Universal Transverse Mercator capable de rendre de manière raisonnable les zones polaires et proches, ce qui la distingue du Mercator "classique". Cependant comme une projection globale elle est peu utile, les distorsions frappent les zones éloignées du méridien central.
Elle est utilisée souvent (parfois elle est officielle, par ex. aux États Unis, et par l'Otan). On divise la sphère en 120 zones, et on applique l'UTM à chaque zone. Les standards prévoient aussi 2 projections stéréographiques pour les zones polaires. Cette dernière est une projection azimutale, mais conforme (non pas photographique).

 Si le cône est tangent à la sphère, un parallèle (l'isomètre central) et son voisinage est rendu fidèlement, plus loin les écarts augmentent. Mais on peut, comme à gauche, prévoir une configuration sécante, qui est exacte sur deux méridiens, et la zone entre les deux est assez correcte.
Si le cône est tangent à la sphère, un parallèle (l'isomètre central) et son voisinage est rendu fidèlement, plus loin les écarts augmentent. Mais on peut, comme à gauche, prévoir une configuration sécante, qui est exacte sur deux méridiens, et la zone entre les deux est assez correcte.
 Le dessin central est la vue polaire, et le droit : équatoriale. On voit que le rayon \(r\) du parallèle à la latitude \(\varphi\) est \(r=R\cos(\varphi)\), dépend de la latitude. Donc, la longueur du segment horizontal sera \(R\cos(\varphi)d\lambda\). Par contre, le segment vertical a toujours la longueur \(R d\varphi\). Donc, \(dS = R^2 \cos(\varphi) d\lambda \cdot d\varphi\). Dans l'avenir nous prendrons typiquement \(R=1\).
Si on effectue une transformation \(x=x(\lambda,\varphi)\) et \(y=y(\lambda,\varphi)\), où \((x,y)\) sont considérées cartésiennes, \(dS = dx dy\). La transformation de l'élément surfacique est proportionnelle au Jacobien de la transformation (un minimum de connaissance de mathématiques s'impose...)
Le dessin central est la vue polaire, et le droit : équatoriale. On voit que le rayon \(r\) du parallèle à la latitude \(\varphi\) est \(r=R\cos(\varphi)\), dépend de la latitude. Donc, la longueur du segment horizontal sera \(R\cos(\varphi)d\lambda\). Par contre, le segment vertical a toujours la longueur \(R d\varphi\). Donc, \(dS = R^2 \cos(\varphi) d\lambda \cdot d\varphi\). Dans l'avenir nous prendrons typiquement \(R=1\).
Si on effectue une transformation \(x=x(\lambda,\varphi)\) et \(y=y(\lambda,\varphi)\), où \((x,y)\) sont considérées cartésiennes, \(dS = dx dy\). La transformation de l'élément surfacique est proportionnelle au Jacobien de la transformation (un minimum de connaissance de mathématiques s'impose...)

 (La projection à gauche est similaire à Lambert conique conforme, utilisé officiellement pour la France).
Digression. Une observation "sociologique". Parmi une soixantaine de pages Web qui parlent de projections conformes, peut-être une ou deux contiennent des informations sérieuses (mathématiquement correctes et complètes, et pratiquement utiles : constructives, et pas trop difficiles)... Et pourtant, ce n'est aucune magie.
Si les angles sont conservés, alors un petit carré doit rester carré. Localement, modulo corrections d'ordre supérieur, le carré peut subir une rotation et une dilatation, c'est tout. Mais on ne doit pas utiliser directement les coordonnées \((\lambda,\varphi)\), car le "carré" implique l'usage des distances. Or, \(d\varphi\), la distance verticale est OK, mais \(d\lambda\) – non, la longueur du segment \(d\lambda\) se retrécit quand \(\varphi\) grandit, donc introduisons \(d\bar{\lambda} = d\lambda\cdot\cos(\varphi)\).
En général, la transformation sera conforme, si la matrice de Jacobi J :
(La projection à gauche est similaire à Lambert conique conforme, utilisé officiellement pour la France).
Digression. Une observation "sociologique". Parmi une soixantaine de pages Web qui parlent de projections conformes, peut-être une ou deux contiennent des informations sérieuses (mathématiquement correctes et complètes, et pratiquement utiles : constructives, et pas trop difficiles)... Et pourtant, ce n'est aucune magie.
Si les angles sont conservés, alors un petit carré doit rester carré. Localement, modulo corrections d'ordre supérieur, le carré peut subir une rotation et une dilatation, c'est tout. Mais on ne doit pas utiliser directement les coordonnées \((\lambda,\varphi)\), car le "carré" implique l'usage des distances. Or, \(d\varphi\), la distance verticale est OK, mais \(d\lambda\) – non, la longueur du segment \(d\lambda\) se retrécit quand \(\varphi\) grandit, donc introduisons \(d\bar{\lambda} = d\lambda\cdot\cos(\varphi)\).
En général, la transformation sera conforme, si la matrice de Jacobi J :